Bài 3: Giải bài toán bằng cách lập phương trìnhMột vòi nước chảy vào bể không có nước. Cùng lúc đó một vòi nước khác chảy từ bể ra. Mỗi giờ lượng nước vòi chảy ra bằng 4/5 lượng nước chảy vào. Sau 5 giờ thì bên trong bể đạt tới 1/8 dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu thì đầy...
Đọc tiếp
Bài 3: Giải bài toán bằng cách lập phương trình
Một vòi nước chảy vào bể không có nước. Cùng lúc đó một vòi nước khác chảy từ bể ra. Mỗi giờ lượng nước vòi chảy ra bằng 4/5 lượng nước chảy vào. Sau 5 giờ thì bên trong bể đạt tới 1/8 dung tích bể. Hỏi nếu bể không có nước mà chỉ mở vòi chảy vào thì sau bao lâu thì đầy bể?
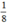dung tích bể nên ta có phương trình: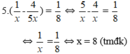
Gọi dung tích bể vòi chảy vào mỗi giờ là \(x\) \(\left(x>0\right)\)
Dung tích bể vòi chảy ra mỗi giờ là \(\dfrac{4}{5}x\)
Dung tích bể vòi chảy vào sau 5 giờ là \(5x\)
Dung tích bể vòi chảy ra sau 5 giờ là \(5.\dfrac{4}{5}x=4x\)
Vì sau 5 giờ thì bên trong bể đạt \(\dfrac{1}{8}\) dung tích bể nên ta có phương trình:
\(5x-4x=\dfrac{1}{8}\)
\(x=\dfrac{1}{8}\)
Vậy mỗi giờ lượng nước chảy vào bể đạt \(\dfrac{1}{8}\) dung tích bể
Thời gian bể đầy nước nếu chỉ mở vòi chảy vào là: \(1:\dfrac{1}{8}=8\) ( giờ )
mik xik loi mik ko bt lm