tìm các cạnh của một tam giác vuông biết đường cao và trung tuyến ứng với cạnh huyền lần lượt là 4cm và 5cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
Nguyễn Minh Quang
Giáo viên
11 tháng 8 2021
ta có \(BC=2AM=2\times5=10cm\)
ta có \(MH=\sqrt{AM^2-AH^2}=\sqrt{5^2-4^2}=3cm\)
nên \(HB=MB-MH=5-4=1cm\) mà ta có \(AB^2=BH.BC=1.10\Rightarrow AB=\sqrt{10}\Rightarrow AC=\sqrt{BC^2-AB^2}=3\sqrt{10}\left(cm\right)\)
10 tháng 1 2022
độ dài cạnh huyền là:
5x2=10(cm)
độ dài cạnh góc vuông thứ hai là:
\(\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
độ dài đường cao là:
\(5\cdot5\sqrt{3}:10=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
TD
19 tháng 7 2017
áp dụng hệ thức: \(\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}\)=> \(\frac{1}{h^2}=\frac{1}{25}+\frac{1}{49}=\frac{74}{1225}\)=>\(h=\frac{35\sqrt{74}}{74}\left(cm\right)\)
áp dụng hệ thức: ab=hc (c là cạnh huyền) => \(35=c\frac{35\sqrt{74}}{74}\)=>\(c=\sqrt{74}\)(cm)
áp dụng hệ thức hình chiếu: =>a'=\(\frac{25\sqrt{74}}{74}\left(cm\right)\)=>b'=\(\frac{49\sqrt{74}}{74}\left(cm\right)\)
11 tháng 7 2021
k mk nha
đúng
Bài giải:
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lí Pitago ta có:
a2 = 72 + 242 = 49 + 576 = 625
Nên a = 25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là 12,5cm.
15 tháng 5 2023
\(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Xét ΔABC vuông tại A có sin C=AB/BC=5/13
nên góc C=22 độ
=>góc B=68 độ
AM=13/2=6,5cm
AH=5*12/13=60/13cm
PT
1
CM
9 tháng 1 2019
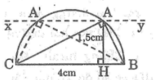
*cách vẽ:
- Vẽ đoạn thẳng BC = 4cm
-Vẽ nửa đường tròn đường kính BC
-Vẽ đường thẳng xy nằm trên nửa mặt phẳng chứa nửa đường tròn đường kính BC và xy // BC ,cách BC một khoảng bằng 1,5cm
- Đường thẳng xy cắt nửa đường tròn đường kính BC tại A và A’.Nối AB, AC, A’B, A’C ta được tam giác ABC cần vẽ
*Chứng minh:
Vì xy cách BC một khoảng bằng 1,5cm nhỏ hơn BC/2 = 2cm nên xy cắt nửa đường tròn đường kính BC
Ta lại có tam giác ABC nội tiếp trong nửa đường tròn đường kính BC nên
góc (BAC) = 90 °
Mặt khác AH ⊥ BC và AH =1,5cm.
Độ dài cạnh huyền là: \(5.2=10\left(cm\right)\)
Gọi độ dài hai cạnh góc vuông lần lượt là \(a,b\left(cm\right);a,b>0\).
Ta có: \(ab=4.10=40\)
\(a^2+b^2=10^2=100\Rightarrow\left(a+b\right)^2=100+2ab=180\Rightarrow a+b=6\sqrt{5}\)
Do đó \(a,b\)là hai nghiệm của phương trình \(X^2-6\sqrt{5}X+40=0\)
\(\Leftrightarrow\left(X-4\sqrt{5}\right)\left(X-2\sqrt{5}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}X=4\sqrt{5}\\X=2\sqrt{5}\end{cases}}\)
Do đó độ dài hai cạnh góc vuông lần lượt là \(4\sqrt{5}\left(cm\right),2\sqrt{5}\left(cm\right)\).