Bài 3: Cho hàm số f(x) = ax2 + bx + c (a, b, c ∈ Z). Biết f(-1) ⋮ 3; f(0) ⋮ 3; f(1) ⋮ 3. Chứng minh rằng a, b, c đều chia hết cho 3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PV
17 tháng 2 2024
Sao ra được chỗ dấu = thứ 2. 5ax^+(3b-6a)x+c-3b/√2x-3 á, thắc mắc
CM
18 tháng 12 2019
Ta có f x = 4 x 2 + 4 x + 3 2 x + 1 dx
= ∫ 2 x + 1 + 2 2 x + 1 d x = x 2 + x + ln x + 1 + C
Do f(0) = 1 nên c = 1. Suy ra f x = x 2 + x + ln 2 x + 1 + 1
Vậy a : b : c = 1 : 1 : 1
Đáp án B
16 tháng 4 2022
7a+b=0 => b=-7a
=> f(x)=ax2+bx+c=ax2-7ax+c
=> f(10) = 102a - 7a.10 + c = 100a-70a+c= 30a+c
f(-3) = (-3)2a - 7.a .(-3) + c = 9a+21a+c=30a+c
=> f(10).f(-3) = (30a+c)2 là số chính phương nên không thể là số âm
29 tháng 11 2023
Bài 4:
\(f\left(5\right)-f\left(4\right)=2019\)
=>\(125a+25b+25c+d-64a-16b-4c-d=2019\)
=>\(61a+9b+21c=2019\)
\(f\left(7\right)-f\left(2\right)\)
\(=343a+49b+7c+d-8a-4b-2c-d\)
\(=335a+45b+5c\)
\(=5\left(61a+9b+21c\right)=5\cdot2019\) là hợp số
UN
0
UN
0
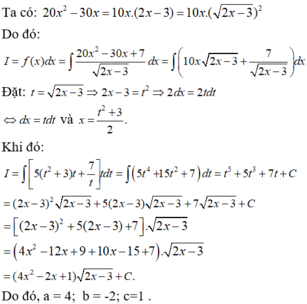
ta có \(\hept{\begin{cases}f\left(-1\right)=a-b+c\\f\left(0\right)=c\\f\left(1\right)=a+b+c\end{cases}}\)
vậy c chia hết cho 3 và \(\hept{\begin{cases}a+b\\a-b\end{cases}\text{ chia hết cho 3}}\)
cộng lại ta có 2a chia hết cho 3 hay a chia hết cho 3
lấy hiệu ta có 2b chia hết cho3 hay b chia hết cho 3
????????