Question

[Neet]

1) tìm các số TN n (2000<n<60000) sao cho mỗi số đó thì a_n=\(\sqrt[3]{54756+5n}\) cũng là số TN

2)tính S phần gạch sọc (đen đen ý )giới hạn bởi các cung tròn và cạnh của tg đều ABC có cạnh dài \(\sqrt{20,16}cm\)

hình hơi xấu i hope everyone thông cảm

Answer 1

[Akai Haruma]

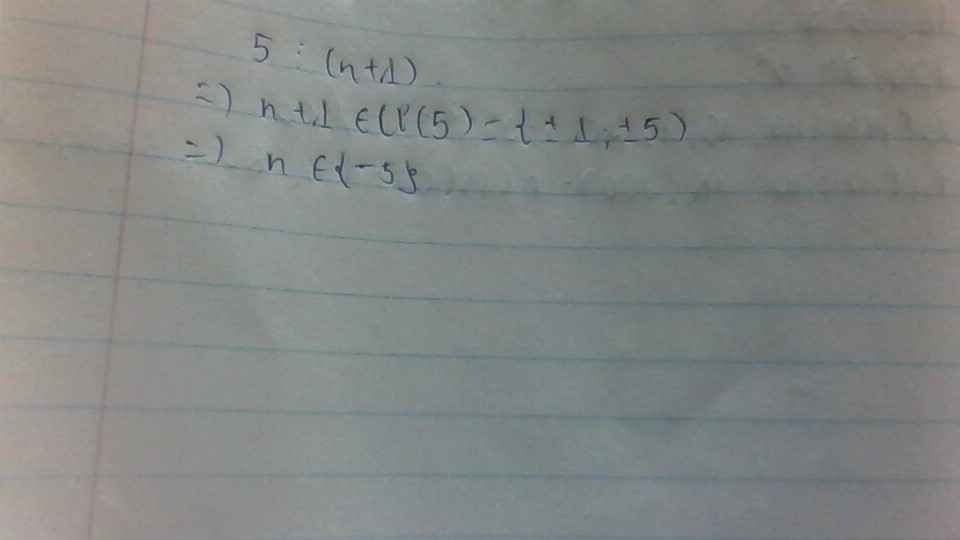
Bài 1:

Vì \(n\in [2000,60000]\) nên \(41\leq a_n=\sqrt[3]{54756+5n}\leq 70\)

Xét \(a_n^3=54756+5n\equiv 1\pmod 5\Leftrightarrow (a_n-1)(a_n^2+a_n+1)\equiv 0\pmod 5\)

Ta có \(4(a_n^2+a_n+1)=(2a_n+1)^2+3\). Vì scp chia $5$ luôn dư $0,1,4$ nên hiển nhiên \(4(a_n^2+a_n+1)\) không chia hết cho $5$, hay \(a_n^2+a_n+1\) không chia hết cho $5$

Do đó \(a_n-1\vdots 5\), hay $a_n$ chia $5$ dư $1$

Kết hợp với \(a_n\in[41,70]\) ta dễ dàng giới hạn được giá trị của $a_n$

\(a_n\in \left \{ 41,46,51,56,61,66 \right \}\) \(\Rightarrow n\in \left \{ 2833,8516,15579,24172,34445,46548 \right \}\)

Answer 2

[Akai Haruma]

Bài 2:

Để cho gọn, đặt \(a=\sqrt{20,16}\)

Tính toán đơn giản \(AH=\sqrt{AB^2-BH^2}=a^2-\frac{a^2}{4}\Rightarrow AH=\frac{\sqrt{3}}{2}a\)

\(\Rightarrow S_{ABC}=\frac{AH.BC}{2}=\frac{\sqrt{3}}{4}a^2\)

Hình được tô trắng gọi là hình viên phân. Gọi giao điểm ba đường cao của tam giác là $I$. Lấy điểm \(O\) sao cho \(\triangle OAI\) là tam giác đều. Ta có \(OAI\) chính là hình quạt cùa hình tròn tâm $O$ bán kính \(\frac{2AH}{3}=\frac{\sqrt{3}}{3}a\)

Do đó diện tích nửa hình viên phân là:

\(\frac{1}{2}S_{\text{vp}}=\frac{1}{6}S_{(O)}-S_{OAI}=\frac{\pi R^2}{6}-\frac{\sqrt{3}a^2}{12}=\frac{\pi a^2}{18}-\frac{\sqrt{3}a^2}{12}\)

\(\Rightarrow 3S_{\text{vp}}=\frac{\pi a^2}{6}-\frac{\sqrt{3}a^2}{4}\)

\(\Rightarrow S_{\text{cần tìm}}=S_{ABC}-3S_{\text{vp}}=\frac{\sqrt{3}a^2}{4}-\frac{\pi a^2}{6}+\frac{\sqrt{3}a^2}{4}\)

\(\Rightarrow S_{\text{cần tìm}}\approx 6,9\) (đvdt)