cho tam giác DEF có đường trung tuyến DM và EN cắt nhau tại G.biết DM = 9cm.tính DG,GM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
2
HN
5 tháng 5 2019
Xét \(\Delta DEF\)
DM, EN là các đường trung tuyến (gt)
\(DM\cap EN=\left\{G\right\}\)
=> G là trọng tâm của \(\Delta DEF\) (tính chất 3 đường trung tuyến)
=> DG = \(\frac{2}{3}DM\) (tính chất trung tuyến)
=> DG = \(\frac{2}{3}.9\) (thay số)
=> DG = 6 (cm)
HN
5 tháng 5 2019
DG + GM = DM (tính chất cộng đoạn thẳng)
6 + GM = 9 (thay số)
GM = 3 (cm)
15 tháng 5 2023
`\Delta DEF` có:
\(\text{DM}\cap\text{EN}\cap\text{FP}=\text{G}\)
Mà \(\text{DM, EN, FP}\) là các đường trung tuyến
`->`\(\text{G là trọng tâm của }\Delta\text{DEF}\)
A. `GD = 2GM` (đúng)
B. EN = 3GN (đúng)
C. `(GF)/(FP)=1/3` (sai)
`-` Khoảng cách từ trọng tâm đến đỉnh là `2/3` chứ không phải `1/3`.
D. `(EG)/(EN) = 2/3` (đúng)
Xét các đáp án trên `-> C (tm).`
17 tháng 3 2023
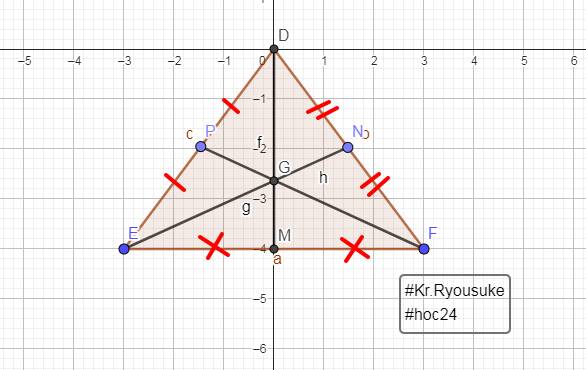
a: G là trọng tâm
=>BG=2/3BD; CG=2/3CE
=>BG=CG
=>DG=GE
b: Xet ΔEBC và ΔDCB có
BC chung
góc ECB=góc DBC
EC=BD
=>ΔEBC=ΔDCB
=>góc ABC=góc ACB
=>ΔACB cân tại A
TH
1
HT
0
17 tháng 4 2023
a) Ta có .
Ta lại có là giao điểm của và là trọng tâm của tam giác
.
Suy ra .
Chứng minh tương tự ta được .
b) Xét tam giác và tam giác có (chứng minh trên);
(hai góc đối đỉnh);
(chứng minh trên).
Do đó (c.g.c)
(hai cạnh tương ứng).
Theo chứng minh trên (hai góc tương ứng).
Mà và ờ vị trí so le trong nên // .
NQ
Nguyễn Quang Đạt
VIP
20 tháng 4 2023
a) Ta có .
Ta lại có là giao điểm của và là trọng tâm của tam giác
.
Suy ra .
Chứng minh tương tự ta được .
b) Xét tam giác và tam giác có (chứng minh trên);
(hai góc đối đỉnh);
(chứng minh trên).
Do đó (c.g.c)
(hai cạnh tương ứng).
Theo chứng minh trên (hai góc tương ứng).
Mà và ờ vị trí so le trong nên // .
đg trung tuyến là gì, mk chưa học cái đó
uk