Cho hình cửu giác đều như hình vẽ. Chứng minh rằng BF = BI + BA.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Các đường thẳng vuông góc với BF là: AB, BC, CD, DA, AC, EF, FG, GH, HE và FH.
b) (ABCD) và (BCGF), (CDHG) và (EFGH), (ADHE) và (ABCD)
Lưu ý: HS có thể liệt kê tên các cặp mặt phẳng khác.
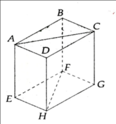

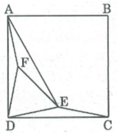
Xét ∆ ADE và ∆ BCE , ta có:
ED = EC (vì AEDC cân tại E)
∠ (ADE) = ∠ (BCE) = 75 0
AD = BC (gt)
Suy ra: ∆ ADE = ∆ BCE (c.g.c)
⇒ AE = BE (1)
* Trong ∆ ADE, ta có:
∠ (AFD) = 180 0 – ( ∠ (FAD) + ∠ (FDA) ) = 180 0 – ( 15 0 + 15 0 ) = 150 0
∠ (AFD) + ∠ (DFE) + ∠ (AFE) = 360 0
⇒ ∠ (AFE) = 360 0 - ( ∠ (AFD) + ∠ (DFE) ) = 360 0 – ( 150 0 + 60 0 ) = 150 0
* Xét ∆ AFD và ∆ AFE, ta có: AF cạnh chung
∠ (AFD) = ∠ (AFE) = 150 0
DE = EF (vì ∆ DFE đều)
Suy ra: ∆ AFD = ∆ AFE (c.g.c) ⇒ AE = AD
Mà AD = AB (gt)
Suy ra: AE = AB (2)
Từ (1) và (2) suy ra: AE = AB = BE
Vậy ∆ AEB đều.

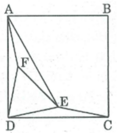
Xét ∆ EDC và ∆ FDA, tacó: ∠ (EDC) = ∠ (FDA) = 15 0
DC = AD (gt)
∠ (ECD) = ∠ (FAD) = 15 0
Suy ra: ∆ EDC = ∆ FDA (g.c.g)
⇒ DE = DF
⇒ ∆ DEF cân tại D
Lại có: ∠ (ADC) = ∠ (FDA) + ∠ (FDE) + ∠ (EDC)
⇒ ∠ (FDE) = ∠ (ADC) -( ∠ (FDA) + ∠ (EDC) )= 90 0 - ( 15 0 + 15 0 ) = 60 0
Vậy ∆ DEF đều.
hình vẽ đâu vậy bạn ????
Hoa Thạch Thảo không phải không biết vẽ mà là không copy qua được -__-