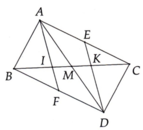
Tam giác ABC ( AB = AC ). Kẻ trung tuyến AM. Kẻ MD _|_ AC, Gọi E trung điểm CD và F trung điểm MD. Chứng minh AF _|_ BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

28 tháng 5 2020
a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )


Xét tam giác DMC có:
F trung điểm MD
E trung điểm DC
=> EF là đường TB mà MC là cạnh đáy
=> EF // MC hay EF // BC (1)
Lại có tam giác ABC cân vì AB = BC, có AM trung tuyến => AM là đường cao => AM _|_ BC (2)
Từ (1) và (2) => EF _|_ AM
Xét tam giác AME có:
MD và EF là đường cao
\(MD\)\(\cap\)EF \(=\left\{F\right\}\)
=> F là trực tâm => AF đường cao => AF _|_ ME (3)
Xét tam giác BDC có:
M trung điểm BC
E trung điểm DC
=> ME là đường TB mà BD là cạnh đáy
=> ME = BD (4)
Từ (3) và (4) => AF _|_ BD (đpcm)