tìm x: a) 9x2 - 6x - 8 =0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 8 2021
b)x2-2x+1=4
⇔(x-1)2=4
\(\Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\)
c)x2-4x+4=9
⇔ (x-2)2=9
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
d)4x2-4x+1=4
⇔ (2x-1)2=4
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=4\\2x-1=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{-3}{2}\end{matrix}\right.\)
e)x2-2x-8=0
⇔ x2-4x+2x-8=0
⇔ x(x-4)+2(x-4)=0
⇔(x-4)(x+2)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
f)9x2-6x-8=0
⇔ 9x2-12x+6x-8=0
⇔ 3x(3x-4)+2(3x-4)=0
⇔ (3x-4)(3x+2)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=\dfrac{-2}{3}\end{matrix}\right.\)
B
1
NH
21 tháng 6 2023
a)
`4(x-2)^2 =4`
`<=>(x-2)^2 =1`
`<=>x-2=1` hoặc `x-2=-1`
`<=>x=3` hoặc `x=1`
b)
`5(x^2 -6x+9)=5`
`<=>(x-3)^2 =1`
`<=>x-3=1`hoặc `x-3=-1`
`<=>x=4` hoặc `x=2`
c)
`4x^2 +4x+1=0`
`<=>(2x+1)^2 =0`
`<=>2x+1=0`
`<=>x=-1/2`
d)
`9x^2 +6x+1=2`
`<=>(3x+1)^2 =2`
\(< =>\left[{}\begin{matrix}3x+1=\sqrt{2}\\3x+1=-\sqrt{2}\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{\sqrt{2}-1}{3}\\x=\dfrac{-\sqrt{2}-1}{3}\end{matrix}\right.\)
18 tháng 8 2021
a) \(7x\left(2x-3\right)-\left(4x^2-9\right)=0\Rightarrow7x\left(2x-3\right)-\left(2x-3\right)\left(2x+3\right)=0\Rightarrow\left(2x-3\right)\left(7x-2x+3\right)=0\Rightarrow\left[{}\begin{matrix}2x-3=0\\5x+3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{5}\end{matrix}\right.\)
b) \(\left(2x-7\right).\left(x-2\right)\left(x^2-4\right)=0\Rightarrow\left(2x-7\right)\left(x-2\right)^2\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}2x-7=0\\\left(x-2\right)^2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\\x=-2\end{matrix}\right.\)
c)\(\left(9x^2-25\right)-\left(6x-10\right)=0\Rightarrow\left(3x-5\right)\left(3x+5\right)-2\left(3x-5\right)=0\Rightarrow\left(3x-5\right)\left(3x+5-2\right)=0\Rightarrow\left[{}\begin{matrix}3x-5=0\\3x+3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=1\end{matrix}\right.\)
18 tháng 8 2021
a: Ta có: \(7x\left(2x-3\right)-\left(4x^2-9\right)=0\)
\(\Leftrightarrow7x\left(2x-3\right)-\left(2x-3\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{3}{5}\end{matrix}\right.\)
b: Ta có: \(\left(2x-7\right)\left(x-2\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)^2\cdot\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\\x=-2\end{matrix}\right.\)
c: Ta có: \(\left(9x^2-25\right)-\left(6x-10\right)=0\)
\(\Leftrightarrow\left(3x-5\right)\left(3x+5-2\right)=0\)
\(\Leftrightarrow\left(3x-5\right)\left(3x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-1\end{matrix}\right.\)
M
3
2
12 tháng 5 2022
`M=-9x^2+6x-3`
`M=-(9x^2-6x+3)`
`M=-(9x^2-6x+1+2)`
`M=-(3x-1)^2-2`
Vì `-(3x-1)^2 <= 0 AA x`
`<=>-(3x-1)^2-2 <= -2 AA x`
Hay `M <= -2 AA x`
Dấu "`=`" xảy ra `<=>(3x-1)^2=0<=>3x-1=0<=>x=1/3`
Vậy `GTLN` của `M` là `-2` khi `x=1/3`
12 tháng 5 2022
\(M=-9x^2+6x-3\)
\(M=-\left(9x^2-6x+3\right)\)
\(M=-\left[\left(3x-1\right)^2+2\right]\)
\(M=-\left(3x-1\right)^2-2\)
\(\Rightarrow Max_M=-2\) khi \(3x-1=0\)
\(\Leftrightarrow x=\dfrac{1}{3}\)
9 tháng 5 2022
Bài 1:
a: \(x^2+6x+8=0\)
=>(x+2)(x+4)=0
=>x=-2 hoặc x=-4
b: \(9x^2-6x+1=0\)
=>(3x-1)2=0
=>3x-1=0
hay x=1/3
HP
9 tháng 5 2022
Câu 1:
a. x2 + 6x + 8 = 0
\(\Delta'=3^2-8=1>0\)
Do \(\Delta'>0\) nên phương trình có 2 nghiệm phân biệt:
\(x_1=\dfrac{-3+\sqrt{1}}{1}=-2\)
\(x_2=\dfrac{-3-\sqrt{1}}{1}=-4\)
b. 9x2 - 6x + 1 = 0
\(\Delta'=\left(-3\right)^2-9.1=0=0\)
Do \(\Delta'=0\) nên phương trình có nghiệm kép:
\(x_1=x_2=\dfrac{3}{9}=\dfrac{1}{3}\)
A
2
13 tháng 2 2022
\(a,\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\ b,4x^2-1=0\\ \Leftrightarrow\left(2x-1\right)\left(2x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=0\\2x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\end{matrix}\right.\)
\(c,x^2-4x+3=0\\ \Leftrightarrow x^2-3x-x+3=0\\ \Leftrightarrow x\left(x-3\right)-\left(x-3\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-3=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
\(d,9x^2-6x+1=0\\ \Leftrightarrow\left(3x-1\right)^2=0\\ \Leftrightarrow3x-1=0\\ \Leftrightarrow x=\dfrac{1}{3}\)
26 tháng 10 2021
a: \(\Leftrightarrow x\left(x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
c: \(\Leftrightarrow\left(x-1\right)\left(3x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
26 tháng 10 2021
a) \(x^2-6x=0\\ \Leftrightarrow x\left(x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)
b) \(\Leftrightarrow\left(3x-1-x-5\right)\left(3x-1+x+5\right)=0\\ \Leftrightarrow\left(2x-6\right)\left(4x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
c) \(9x^2\left(x-1\right)=x-1\\ \Leftrightarrow\left(9x^2-1\right)\left(x-1\right)=0\\ \Leftrightarrow\left(3x-1\right)\left(3x+1\right)\left(x-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\\x=1\end{matrix}\right.\)
d) \(x^2-4=\left(x-2\right)^2\\ \Leftrightarrow\left(x-2\right)\left(x+2-x+2\right)=0\\ \Leftrightarrow4\left(x-2\right)=0\\ \Leftrightarrow x=2\)
e) \(\Leftrightarrow\left(x+3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\\x=-2\end{matrix}\right.\)
f) \(x^3-0,36=0\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{3}{5}\\x=\dfrac{3}{5}\end{matrix}\right.\)
g) \(\Leftrightarrow\left(5x-1\right)\left(x-2018\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{5}\\x=2018\end{matrix}\right.\)
h) \(\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)
NN
1
14 tháng 10 2021
\(9x^2-6x+20\)
\(=9x^2-6x+1+19\)
\(=\left(3x-1\right)^2+19>0\forall x\)
HP
21 tháng 9 2021
a. 9x2 - 6x - 3 = 0
<=> 3(3x2 - 2x - 1) = 0
<=> 3(3x2 - 3x + x - 1) = 0
<=> \(3\left[3x\left(x-1\right)+\left(x-1\right)\right]=0\)
<=> 3(3x + 1)(x - 1) = 0
<=> \(\left[{}\begin{matrix}3x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{3}\\x=1\end{matrix}\right.\)
b. (2x + 1)2 - 4(x + 2)2 = 9
<=> (2x + 1)2 - \(\left[2\left(x+2\right)\right]^2=9\)
<=> (2x + 1 - 2x - 4)(2x + 1 + 2x + 4) = 9
<=> -3(4x + 5) = 9
<=> 4x + 5 = -3
<=> 5 + 3 = -4x
<=> -4x = 8
<=> -x = 2
<=> x = -2
21 tháng 9 2021
a) \(\Leftrightarrow\left(9x^2-6x+1\right)-4=0\)
\(\Leftrightarrow\left(3x-1\right)^2-4=0\)
\(\Leftrightarrow3\left(x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)
b) \(\Leftrightarrow4x^2+4x+1-4x^2-16x-16=9\)
\(\Leftrightarrow12x=-24\Leftrightarrow x=-2\)
c) \(\Leftrightarrow3x^2-6x+3-3x^2+15x=21\)
\(\Leftrightarrow9x=18\Leftrightarrow x=2\)
d) \(\Leftrightarrow x^2+6x+9-x^2-4x+32=1\)
\(\Leftrightarrow2x=-40\Leftrightarrow x=-20\)
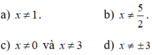
Ta có :
\(9x^2-6x-8=0\)
\(x.\left(9x-6\right)=8\)
Lập bảng xét là xong ok