giải phương trình
2x3-5x2+5x-2=0
cứu mik nha các bạn mik cần gấp nắm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 2 2021
Câu 1:
a) Ta có: 7x+21=0
\(\Leftrightarrow7x=-21\)
hay x=-3
Vậy: S={-3}
b) Ta có: 3x-2=2x-3
\(\Leftrightarrow3x-2-2x+3=0\)
\(\Leftrightarrow x+1=0\)
hay x=-1
Vậy: S={-1}
c) Ta có: 5x-2x-24=0
\(\Leftrightarrow3x=24\)
hay x=8
Vậy: S={8}
Câu 2:
a) Ta có: \(\left(2x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-1\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)
Vậy: \(S=\left\{-\dfrac{1}{2};1\right\}\)
b) Ta có: \(\left(2x-3\right)\left(-x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\-x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\-x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=7\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{3}{2};7\right\}\)
c) Ta có: \(\left(x+3\right)^3-9\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[\left(x+3\right)^2-9\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x+3-3\right)\left(x+3+3\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=-6\end{matrix}\right.\)
Vậy: S={0;-3;-6}
1 tháng 1 2017
_không có nghiệm bạn ơi _
<=> 5x2 + 7y2 =-100
Mà 5x2 >= 0 với mọi x thuộc R; 5y2 => 0 với mọi y thuộc R
DL
22 tháng 7 2017
\(x^2-5x+6=\left(x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=2\end{cases}}}\)
22 tháng 7 2017
1, <=>x^2-x-2 = x^2-4
<=>x^2-4-x^2+x+2 = 0
<=> x-2 = 0
<=> x=2
2, <=> (x-2).(x-3)=0
<=> x-2 = 0 hoặc x-3 = 0
<=> x=2 hoặc x=3
21 tháng 3 2023
a)\(\left(5x+2\right)\left(2x-6\right)=0\\ \left\{{}\begin{matrix}5x+2=0\Leftrightarrow5x=-2\Leftrightarrow x=\dfrac{-2}{5}\\2x-6=0\Leftrightarrow2x=6\Leftrightarrow x=\dfrac{6}{2}=3\end{matrix}\right.\)
b)\(\dfrac{5x}{2x+2}+1=\dfrac{8}{x+1}\\ \Leftrightarrow\dfrac{5x}{2\left(x+1\right)}+1=\dfrac{8}{x+1}\\ \Leftrightarrow\dfrac{5x+2\left(x+1\right)}{2\left(x+1\right)}=\dfrac{2\cdot8}{2\left(x+1\right)}\\ \Leftrightarrow5x+2\left(x+1\right)=16\\ \Leftrightarrow5x+2x+2=16\\ \Leftrightarrow5x+2x=16-2\\ \Leftrightarrow7x=14\\ \Leftrightarrow x=\dfrac{14}{7}=2\)
21 tháng 3 2023
a, <=>5x+2=0<=>x=-2/5
<=>2x-6=0<=>x=6/2=3
mik có tí việc ko lm hết cho bn đc xl
CM
22 tháng 3 2018
2x3 + 5x2 – 3x = 0
⇔ x(2x2 + 5x – 3) = 0
⇔ x.(2x2 + 6x – x – 3) = 0
⇔ x. [2x(x + 3) – (x + 3)] = 0
⇔ x.(2x – 1)(x + 3) = 0
⇔ x = 0 hoặc 2x – 1 = 0 hoặc x + 3 = 0
+ 2x – 1 = 0 ⇔ 2x = 1 ⇔ x = 1/2.
+ x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm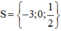 
22 tháng 7 2017
a,(x + 6)(3x +1) + x+6 = 0
(x+6)(3x +2)=0
x= -6
x= -2/3
b, x= -4 hoăc x =-8/5
22 tháng 7 2017
a,(x+6)(3x+1)+x+6=0
=>(x+6)(3x+2)=0
=>x+6=0 hoặc 3x+2=0
=>x=-6 hoặc x=-2/3
b,(x+4)(5x+9)-x-4=0
=>(x+4)(5x+8)=0
=>x+4=0 hoặc 5x+8=0
=>x=-4 hoặc x=-8/5
14 tháng 8 2021
\(\sqrt{4x^2-4x+9}=3\\ \Rightarrow4x^2-4x+9=9\\ \Rightarrow4x\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
15 tháng 8 2021
Ta có: \(\sqrt{4x^2-4x+9}=3\)
\(\Leftrightarrow4x^2-4x=0\)
\(\Leftrightarrow4x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(2x^3-5x^2+5x-2=0\)
\(\Leftrightarrow2\left(x-1\right)\left(x^2+x+1\right)-5x\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2+2x+2-5x\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2-3x+2\right)=0\)
\(\Leftrightarrow\left[\begin{matrix}x-1=0\\x^2-3x+2=0\left(loai\right)\end{matrix}\right.\)\(\Leftrightarrow x=1\)
\(2x^3-5x^2+5x-2=0\)
\(\Leftrightarrow2x^3-2x^2-3x^2+3x+2x-2=0\)
\(\Leftrightarrow2x^2\left(x-1\right)-3x\left(x-1\right)+2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(x^2-2x+1\right)+\left(x^2-x+1\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(x-1\right)^2+\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\right]=0\)
\(\Leftrightarrow\left[\begin{matrix}x-1=0\\\left(x-1\right)^2+\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}x=1\\Ta luôn có: \left(x-1\right)^2\ge0; \left(x-\frac{1}{2}\right)^2\ge0; \frac{3}{4}>0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}x=1\\Pt vô nghiệm\end{matrix}\right.\)
Vậy tập nghiệm của pt là S={1}