"Tìm GTLN
a A= -x2+4x+6
b B= -x2-3x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
D
1
21 tháng 10 2021
a: Ta có: \(B=x^2-4x+6\)
\(=x^2-4x+4+2\)
\(=\left(x-2\right)^2+2\ge2\forall x\)
Dấu '=' xảy ra khi x=2
LD
1
21 tháng 9 2021
2) \(A=-x^2-y^2+2x-6y+9=-\left(x^2-2x+1\right)-\left(y^2+6y+9\right)+19=-\left(x-1\right)^2-\left(y+3\right)^2+19\)
\(maxA=19\Leftrightarrow\)\(\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
13 tháng 10 2021
Bài 1:
$A=(9x^2-5x)+(5y^2+3y)$
$=[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]+5(y^2+\frac{3}{5}y+\frac{3^2}{10^2})-\frac{103}{90}$
$=(3x-\frac{5}{6})^2+5(y+\frac{3}{10})^2-\frac{103}{90}$
$\geq \frac{-103}{90}$
Vậy $A_{\min}=\frac{-103}{90}$. Giá trị này đạt tại $3x-\frac{5}{6}=y+\frac{3}{10}=0$
$\Leftrightarrow (x,y)=(\frac{5}{18}, \frac{-3}{10})$
AH
Akai Haruma
Giáo viên
13 tháng 10 2021
Bài 2:
a.
$-A=4x^2+5y^2-8xy-10y-12$
$=(4x^2-8xy+4y^2)+(y^2-10y+25)-37$
$=(2x-2y)^2+(y-5)^2-37\geq -37$
$\Rightarrow A\leq 37$
Vậy $A_{\max}=37$. Giá trị này đạt tại $2x-2y=y-5=0$
$\Leftrightarrow x=y=5$
b.
$-B=3x^2+16y^2+8xy+5x-2$
$=(x^2+16y^2+8xy)+2(x^2+\frac{5}{2}x+\frac{5^2}{4^2})-\frac{41}{8}$
$=(x+4y)^2+2(x+\frac{5}{4})^2-\frac{41}{8}$
$\geq \frac{-41}{8}$
$\Rightarrow B\leq \frac{41}{8}$
Vậy $B_{\max}=\frac{41}{8}$. Giá trị này đạt tại $x+4y=x+\frac{5}{4}=0$
$\Leftrightarrow x=\frac{-5}{4}; y=\frac{5}{16}$
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 8 2024
A = - 3\(x\).(\(x-5\)) + 3(\(x^2\) - 4\(x\)) - 3\(x\) - 10
A = - 3\(x^2\) + 15\(x\) + 3\(x^2\) - 12\(x\) - 3\(x\) - 10
A = (- 3\(x^2\) + 3\(x^2\)) + (15\(x\) - 12\(x\) - 3\(x\)) - 10
A = 0 + (3\(x-3x\)) - 10
A = 0 - 10
A = - 10
17 tháng 7 2023
\(A=x^2-4x+20=x^2-4x+4+16=\left(x-2\right)^2+16\)
Do \(\left(x-2\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2+16\ge16\)
\(\Rightarrow Min\left(A\right)=16\)
\(B=x^2-3x+7=x^2-3x+\dfrac{9}{4}-\dfrac{9}{4}+7=\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\)
Do \(\left(x-\dfrac{3}{2}\right)^2\ge0\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
\(\Rightarrow Min\left(B\right)=\dfrac{19}{4}\)
\(C=-x^2-10x+70=-\left(x^2+10x+25\right)+25+70=-\left(x-5\right)^2+95\)
Do \(-\left(x-5\right)^2\le0\)
\(\Rightarrow-\left(x-5\right)^2+95\le95\)
\(\Rightarrow Max\left(C\right)=95\)
\(D=-4x^2+12x+1=-\left(4x^2-12x+9\right)+9+1=-\left(2x-3\right)^2+10\)
Do \(-\left(2x-3\right)^2\le0\)
\(\Rightarrow-\left(2x-3\right)^2+10\le10\)
\(\Rightarrow Max\left(D\right)=10\)
CM
12 tháng 2 2017
a) Thực hiện rút gọn VT = -2x – 64
Giải phương trình -2x – 64 = 0 thu được x = -32.
b) Thực hiện rút gọn VT = -62 x +12
Giải phương trình -62x + 12 = -50 thu được x = 1.
18 tháng 10 2021
Do câu d mình ko biết làm bởi v mình không làm được
7 tháng 10 2023
`#3107.101107`
a)
`x^2 + 6x + 10`
`= (x^2 + 2*x*3 + 3^2) + 1`
`= (x + 3)^2 + 1`
Vì `(x + 3)^2 \ge 0` `AA` `x`
`=> (x + 3)^2 + 1 \ge 1` `AA` `x`
Vậy, GTNN của bt là 1 khi `(x + 3)^2 = 0`
`<=> x + 3 = 0`
`<=> x = -3`
b)
`4x^2 - 4x + 5`
`= [(2x)^2 - 2*2x*1 + 1^2] + 4`
`= (2x - 1)^2 + 4`
Vì `(2x - 1)^2 \ge 0` `AA` `x`
`=> (2x - 1)^2 + 4 \ge 4` `AA` `x`
Vậy, GTNN của bt là `4` khi `(2x - 1)^2 = 0`
`<=> 2x - 1 = 0`
`<=> 2x = 1`
`<=> x = 1/2`
c)
`x^2 - 3x + 1`
`= (x^2 - 2*x*3/2 + 9/4) - 5/4`
`= (x - 3/2)^2 - 5/4`
Vì `(x - 3/2)^2 \ge 0` `AA` `x`
`=> (x - 3/2)^2 - 5/4 \ge -5/4` `AA` `x`
Vậy, GTNN của bt là `-5/4` khi `(x - 3/2)^2 = 0`
`<=> x - 3/2 = 0`
`<=> x = 3/2`
19 tháng 12 2021
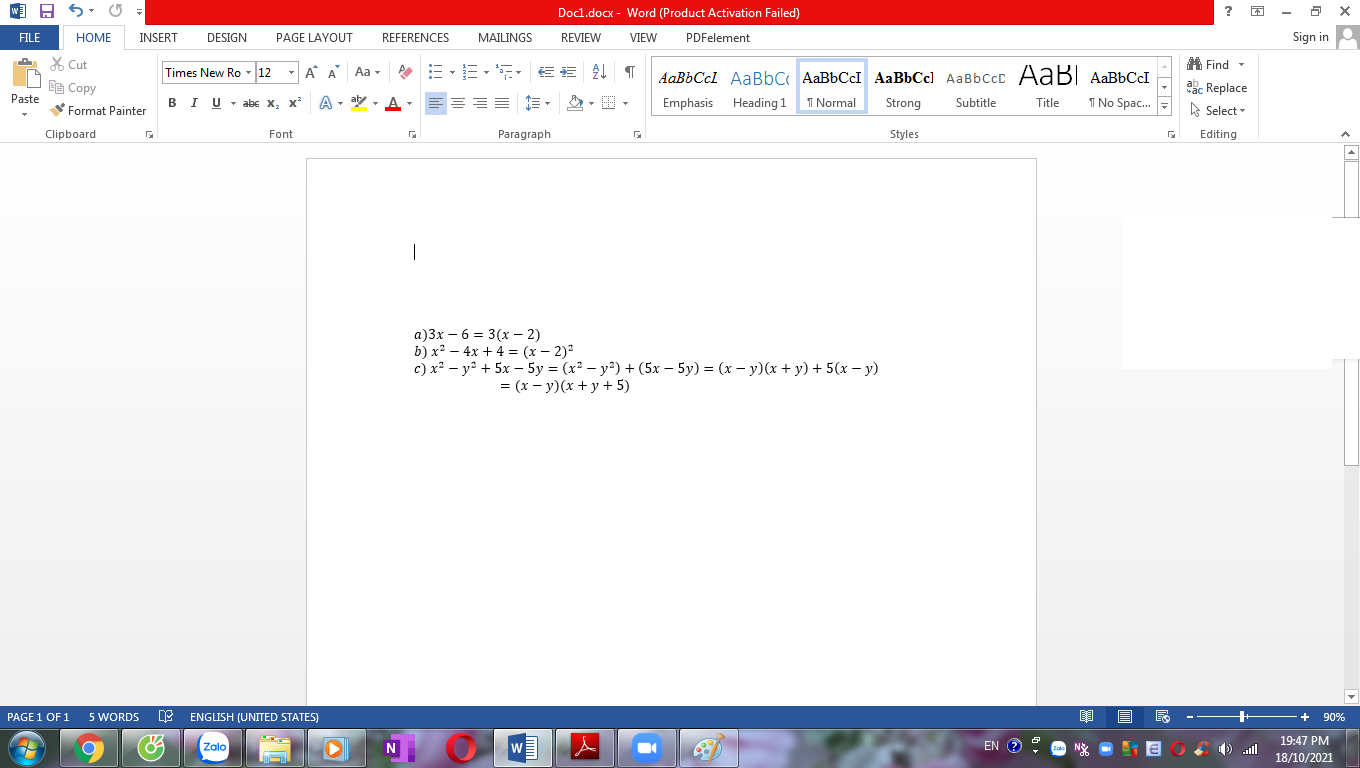
a: \(\Leftrightarrow x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
Trả lời:
a, \(=-x^2+4x+6=-\left(x^2-4x-6\right)=-\left[\left(x^2-4x+4\right)-10\right]=-\left[\left(x-2\right)^2-10\right]\)
\(=-\left(x-2\right)^2+10\le10\forall x\)
Dấu "=" xảy ra khi x - 2 = 0 <=> x = 2
Vậy GTLN của A = 10 khi x = 2
b, \(B=-x^2-3x=-\left(x^2+3x\right)=-\left(x^2+2.x.\frac{3}{2}+\frac{9}{4}-\frac{9}{4}\right)=-\left[\left(x+\frac{3}{2}\right)^2-\frac{9}{4}\right]\)
\(=-\left(x+\frac{3}{2}\right)^2+\frac{9}{4}\le\frac{9}{4}\forall x\)
Dấu "=" xảy ra khi x + 3/2 = 0 <=> x = - 3/2
Vậy GTLN của B = 9/4 khi x = - 3/2
làm hộ mình luôn ạ
https://olm.vn/hoi-dap/detail/1473716361129.html