Hàm số y = log2( 4x- 2x+ m) có tập xác định D= R khi nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 1 2019
Chọn B.
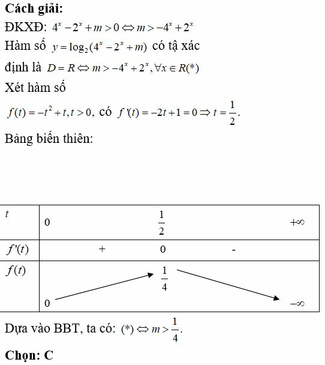
Hàm số có tập xác định là D = R khi và chỉ khi 4x - 2x + m > 0 mọi x. (*)
Đặt t = 2x > 0 khi đó (*) trở thành : t2 – t + m > 0 mọi t > 0.
Hay m > t - t2 mọi t > 0
Ta có 
suy ra 
CM
3 tháng 5 2018
Chọn C
Hàm số
y
=
log
2
(
4
x
-
2
x
+
m
)
có tập xác định là D =
ℝ
Đặt 
Khi đó, bất phương trình (1) trở thành:
Xét hàm số 
Ta có: f'(t) = 2t + 1; f'(t) = 0 ⇔ t = 1 2
Bảng biến thiên:
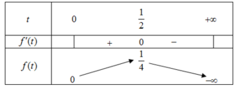
Dựa vào bảng biến thiên, suy ra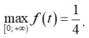 
Từ (*) suy ra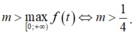 
CM
6 tháng 12 2019
Đáp án D
Hàm số có tập xác định là R <=> 4x – 2x + m > 0, ∀ x ∈ ℝ
⇔ m > 2 x - 4 x ∀ x ∈ ℝ
Đặt t = 2x > 0 => m > t – t2 ∀ t > 0
⇔ m > m a x t > 0 f t ⇔ m > 1 4 .
PT
1
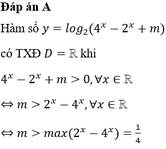
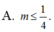
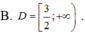
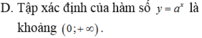
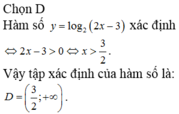
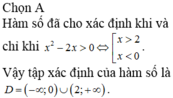
\(\Leftrightarrow4^x-2^x+m>0;\forall x\)
Đặt \(2^x=t>0\Rightarrow t^2-t+m>0;\forall t>0\)
\(\Rightarrow m>-t^2+t\Rightarrow m>\max\limits_{t>0}\left(-t^2+t\right)=\dfrac{1}{4}\)
Vậy \(m>\dfrac{1}{4}\)