Giúp em vs, làm ơn 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
V
0

V
0


2 tháng 9 2021
a: Ta có: \(\left(\dfrac{3}{5}-\dfrac{7}{4}\right):\dfrac{23}{10}\)
\(=\dfrac{12-35}{20}\cdot\dfrac{10}{23}\)
\(=\dfrac{-23\cdot10}{23\cdot20}=-\dfrac{1}{2}\)
b: Ta có: \(\left(-\dfrac{2}{3}+\dfrac{3}{4}\right)^2\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{144}\cdot\dfrac{12}{5}-\dfrac{11}{5}\)
\(=\dfrac{1}{60}-\dfrac{11}{5}=\dfrac{1}{60}-\dfrac{132}{60}=\dfrac{-131}{60}\)

MC
8
SD
0




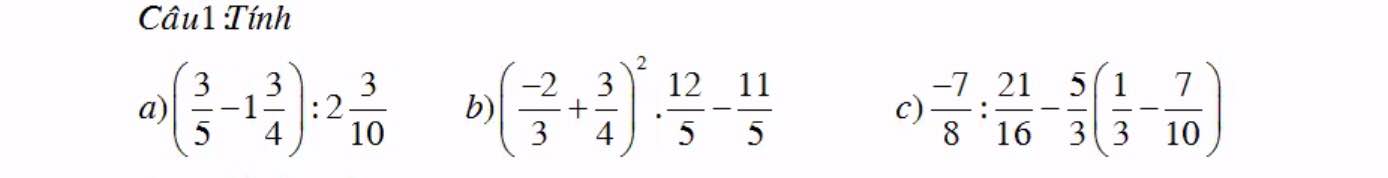





AH vuông góc BC nên các tam giác ABH và ACH là các tam giác vuông tại H
a. Áp dụng hệ thức lượng trong tam giác vuông ABH với đường cao HE:
\(AH^2=AE.AB\) (1)
Áp dụng hệ thức lượng trong tam giác vuông ACH:
\(AH^2=AF.AC\) (2)
(1);(2) \(\Rightarrow AE.AB=AF.AC\)
b. Khi \(AH^2=BH.CH\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\)
Xét hai tam giác vuông ABH và CAH có:
\(\left\{{}\begin{matrix}\dfrac{AH}{CH}=\dfrac{BH}{AH}\\\widehat{AHB}=\widehat{CHA}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta ABH\sim\Delta CAH\left(c.g.c\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{ACH}\)
Mà \(\widehat{ACH}+\widehat{HAC}=90^0\Rightarrow\widehat{BAH}+\widehat{HAC}=90^0\)
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow\) tứ giác AEHF là hình chữ nhật (có 3 góc vuông)
c.
Do AEHF là hình chữ nhật \(\Rightarrow AH=EF\) (hai đường chéo bằng nhau) (3)
Mặt khác \(\widehat{BAC}\) vuông nên tam giác ABC vuông tại A
\(\Rightarrow AB.AC=AH.BC\) (4)
(3);(4) \(\Rightarrow AB.AC=EF.BC\)