cho tam giác vuông có cạnh huyền bằng 25cm và diện tích bằng 125 cm2 . tính chu vi tam giác đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 9 2018
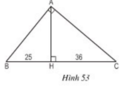
+ BC = BH + HC = 25 + 36 = 61 (cm)
+ ΔABH vuông tại H và ΔABC vuông tại A có:
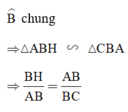
⇒AB2=BH.BC=25.(25+36)=1525
TG
1
12 tháng 2 2017
gọi a và b lần lượt là 2 cạnh góc vuông. ta có hệ pt\(\hept{\begin{cases}a.b=150\cdot2=300\\a^2+b^2=25^2\end{cases}\Leftrightarrow\hept{\begin{cases}a=\frac{300}{b}\\\left(\frac{300}{b}\right)^2+b^2=25^2\end{cases}}\Leftrightarrow\hept{\begin{cases}a=\frac{300}{b}\\b^4-25^2b^2+300^2=0\left(1\right)\end{cases}}}\)
Từ pt (1)=>\(\orbr{\begin{cases}b^2=400\\b^2=225\end{cases}}\Leftrightarrow\orbr{\begin{cases}b=20\Rightarrow a=15\\b=15\Rightarrow a=20\end{cases}}\)( mình không lấy số âm vì đây là độ dài hình học)
Chu vi tam giác 15+20+25=50 cm
22 tháng 8 2020
Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~
VQ
23 tháng 7 2016
Ta có
AM -AH =BC/2 - AH =7
=> BC -2AH =14
=> 2AH = BC-14 (1*)
Mặt khác:
AB+BC+CA= 72
=> AB+CA = 72-BC
=> (AB+AC)^2 = (72-BC)^2
=> AB^2 + CA^2 + 2BC.AH = 72^2 - 144BC + BC^2 (do AB.AC = BC.AH)
=> 2BC.AH = 5184 - 144BC (2*)
Thay (1*) vào (2*)
=> BC(BC-14) = 5184 - 144BC
=> BC^2 + 130BC - 5184 =0
=> sqrt(delta) =194
=> BC = (-130 + 194)/2 = 32
=> AH = (BC-14)/2 = 9
=> S(ABC) =BC.AH/2 = 144 cm^2
30 tháng 7 2017
Gọi a;b là độ dài 2 cạnh góc vuông. Do tam giác vuông; ta có:
Độ dài cạnh huyền = √(a²+b²)
Độ dài đường cao = ab/√(a²+b²)
Do đó chu vi = a+b+√(a²+b²) = 72 (1)
Hiển nhiên trung tuyến phải dài hơn đường cao nên ta có:
1/2.√(a²+b²) -ab/√(a²+b²) = 7
<=> (a²+b²) -2ab = 14√(a²+b²) (2)
Kết hợp (1) và (2) ta được:
a²+b² -2ab = 14.(72-a-b)
<=> a²+b² +14a +14b -1008 = 2ab
<=> (a+b)² +14(a+b) -1008 = 4ab (3)
Từ (1) ta có:
√(a²+b²) = 72-a-b
<=> a²+b² = a²+b²+5184 -144a-144b +2ab
<=> 144(a+b) = 2ab +5184
<=> a+b = ab/72 +36 (4)
Thay (4) vào (3) ta được:
(ab/72 +36)² +14.(ab/72 +36) -1008 = 4ab
<=> (ab +2592)² + 14.72.(ab+2592) -1008.72² = 4.72²ab
<=> (ab)² +5184(ab) +2592² +1008(ab) -4.72²(ab) +14.72.2592 -1008.72² =0
<=> (ab)² -14544(ab) +4105728 =0
<=> (ab -14256)(ab -288) =0
Thử lại:
Nếu: ab = 14256 thì a+b = 14256/72 +36 = 234
Giải pt: X² -234X +14256 =0
Ta thấy: Δ' = 117²-14256 = -567 <0 nên pt vô nghiệm
Nếu: ab = 288 thì a+b = 288/72 +36 = 40
Giải pt: X² -40X² +288 =0
Ta được: X1 = 20 -4√7 ; X2 = 20 +4√7
Đây là độ dài 2 cạnh góc vuông. Từ đây tính được cạnh huyền và đường cao thấy thỏa gt.
Kết luận: Tam giác đã cho có diện tích là 144 (=ab/2)
DN
1
31 tháng 5 2021
Gọi hai cạnh góc vuông của tam giác lần lượt là a;b(a,b>0)
Vì tam giác có cạnh huyền là 5, ta có phương trình: \(a^2+b^2=5^2=25\) (1)
Diện tích tam giác vuông bằng 6m2 ,ta có phương trình: \(\dfrac{1}{2}ab=6\) \(\Leftrightarrow ab=12\)
\(\Leftrightarrow a=\dfrac{12}{b}\) thay vào pt (1) ta được:
\(\left(\dfrac{12}{b}\right)^2+b^2=25\) \(\Leftrightarrow b^4-25b^2+144=0\)\(\Leftrightarrow\left(b^2-16\right)\left(b^2-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}b^2=16\\b^2=9\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}b=4\Rightarrow a=\dfrac{12}{4}=3\\b=3\Rightarrow a=\dfrac{12}{3}=4\end{matrix}\right.\) (thỏa mãn)
Chu vi tam giác vuông là: \(3+4+5=12\) (m)
Vậy ...
DD
Đoàn Đức Hà
Giáo viên
4 tháng 6 2021
Gọi độ dài hai cạnh góc vuông lần lượt là \(a,b\left(cm\right);a,b>0\).
Độ dài cạnh huyền là: \(15.2=30\left(cm\right)\)
Ta có hệ:
\(\hept{\begin{cases}a+b=42\\a^2+b^2=900\end{cases}}\Leftrightarrow\hept{\begin{cases}b=42-a\\a^2+\left(42-a\right)^2=900\end{cases}}\Leftrightarrow\hept{\begin{cases}b=42-a\\a=18;a=24\end{cases}}\Leftrightarrow\orbr{\begin{cases}a=18,b=24\\a=24,b=18\end{cases}}\)
Diện tích tam giác đó là: \(\frac{18.24}{2}=216\left(cm^2\right)\)
PN
0
3 tháng 1 2018
Cạnh của hình tam giác là : 27 : 3 = 9 (cm)
Chiều cao hình tam giác đó là : 45 x 2 : 9 = 10 (cm)
Đáp số : 10 cm
Tk mk nha
bạn ktra lại đề nhé!