Tìm số tự nhiên x lớn nhất, biết rằng 960\(⋮\) x và 540 \(⋮\)x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
HT
0
HT
2
28 tháng 7 2015
Ta có: 216 chia hết cho x => x thuộc Ư(216)
540 chia hết cho x=> x thuộc Ư(540)
1404 chia hết cho x=> x thuộc Ư(1404)
=>x thuộc ƯC(216;540;1404)
216=23*33; 540=22*33*5; 1404=22*33*13
=>ƯC(216;540;1404)=22*33=Ư(108)={1;2;4;6;9;12;18;27;54;108}
mà x thuộc ƯC(216;540;1404) hay x thuộc Ư(108); 50<x<150
=>x thuộc{54;108}
2 tháng 7 2015
Để P lớn nhất thì 540:[x-6] lớn nhất
Do đó [x-6] là số tự nhiên nhỏ nhất (số chia càng nhỏ thì thương càng lớn)
Mà trong 1 phép chia số chia luôn khác 0. Vậy x-6 = 1
x=1+6=7
Giá trị lớn nhất của P chính là 2015 + 540 : 1 = 2015 + 540 = 2555
2 tháng 7 2015
Bài này mới chuẩn nè :
P có GTLN <=> 540 : (x - 6) có GTNN
<=> x - 6 có GTNN. Mà x - 6 ≠ 0 => x - 6 = 1
<=> x = 7. Khi đó P = 2015 + 540 : 1 = 2555 có GTLN tại x = 7
PT
1
TM
0
NL
2
17 tháng 10 2023
\(126=2\cdot3^2\cdot7\)
\(210=2\cdot3\cdot5\cdot7\)
\(\Rightarrow UCLN\left(126,210\right)=2\cdot3\cdot7=42\)
\(\Rightarrow a=42\) là giá trị cần tìm.
17 tháng 10 2023
Ta có:
126=2.32.7
210=2.3.5.7
⇒UCLN(126;210)=2.3.7=42
⇒a=42
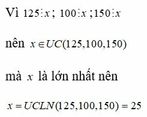
ta có x là UCLN của 960 và 540
mà \(\hept{\begin{cases}960=96\times10=6\times16\times2\times5=2^6\times3\times5\\540=9\times6\times10=2^2\times3^3\times5\end{cases}}\)
Vì vậy \(x=2^2\times3\times5=60\)
6o nhaaaaaaaaa