Cho điểm A nằm trong góc nhọn xOy. Vẽ AH vuông góc với Ox, trên tia đối của tia HA lấy điểm B sao cho HB=HA. Vẽ AK vuông góc với oy, trên tia đối của KA lấy điểm C sao cho KC=KA.
a/ CM:OB=OC
b/Biết góc xOy=t. Tính góc BOC theo t
c/Tìm số đo của t để O là trung điểm của BC
VẼ HÌNH VÀ GHI LỜI GIẢI RA GIÙM MIK, MIK CẦN GẤP THANKS TRC NHA


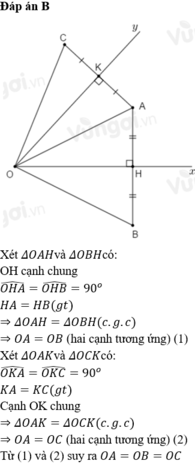
a, Xét \(\Delta\)OKA và \(\Delta\)OKC có:
OK : cạnh chung
CK = AK (gt)
góc OKA = góc OKC = 900
=> \(\Delta\)OKA = \(\Delta\)OKC ( c - g - c)
=> OA = OC ( 2 cạnh tương ứng ) (1)
Xét \(\Delta\)OHA và \(\Delta\)OHB có:
OH : cạnh chung
AH = BH (gt)
góc OHA = góc OHB = 900
=> \(\Delta\)OHA = \(\Delta\)OHB ( c - g - c)
=> OA = OB ( 2 cạnh tương ứng ) (2)
Từ (1), (2)
=> OB = OC (dpcm)
b,
Vì \(\Delta\)OKA = \(\Delta\)OKC ( c - g - c)
=> góc COK = góc AOK = \(\dfrac{1}{2}\)góc AOC
Vì \(\Delta\)OHA = \(\Delta\)OHB ( c - g - c)
=> góc AOH = góc BOH= \(\dfrac{1}{2}\)góc AOB
Ta có:
góc AOC + góc AOB = góc BOC
=> \(\dfrac{1}{2}\)góc AOC + \(\dfrac{1}{2}\)góc AOB = \(\dfrac{1}{2}\)góc BOC
=> góc AOK + góc AOH = \(\dfrac{1}{2}\)góc BOC
=> góc xOy = \(\dfrac{1}{2}\)góc BOC
hay t = \(\dfrac{1}{2}\)góc BOC
=> góc BOC = 2t
Vậy BOC = 2t
Xét ΔOHB(∠H=90) và