Một ô tô chuyển động từ địa điểm A đến địa điểm B cách nhau 90 km. Trong 27 km đầu tàu đi với tốc độ v1 = 25 m/s, đoạn đường còn lại ô tô đi với tốc độ v2 = 20 m/s .
1. Hỏi sau bao lâu ô tô đến B ? 2. Tính tốc độ trung bình của ô tô trên cả quãng đường AB ?Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đổi 10m/s và 15m/s thành 36km/h và 54km/h
a)thời gian đi hêt quãng đuonbgừ thứ nhất
t1=s/v<=> 27/36=0,75h
thời gian đi hết quãng đường t2
t2=s-s1/v2<=>100-27/54=1,35h
thời gian xe sẽ đến B
0,75+1,35=2,1h
b) vtb của ô tô trên cả quãng đường
vtb= s ( tổng í)/t1+t2= 100/2,1=47,61km/h
khang hả =))))))))???????
năm mới vui vẻ nha ;)

Ta có nửa quãng đường đầu ô tô đi được là \(\dfrac{1}{2}\left(km\right)\)
Nửa quãng đường sau ô tô đi được là \(\dfrac{1}{2}\left(km\right)\)
\(\Rightarrow\) Ô tô đi được từ A - B là \(1\left(km\right)\)
Tốc độ trung binh của ô tô trên cả quãng đường AB là
\(v=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{1}{\dfrac{1}{2}:30+\dfrac{1}{2}:60}=40\left(km/h\right)\)

Theo bài ra ta có: quãng đường AB dài 540km => Nửa quãng đường AB dài 270km.
Gọi quãng đường ô tô và xe máy đã đi là S1 và S2.
Trong cùng một thời gian thì quãng đường tỉ lệ thuận với vận tốc.
\(\dfrac{S_1}{V_1}=\dfrac{S_2}{V_2}=t\)
Ta có phương trinh:
\(\dfrac{270-a}{65}=\dfrac{270-a}{40}\Rightarrow t=\dfrac{270}{90}=3h\)
Vậy sau 3 giờ thì ô tô cách M 1 khoảng bằng 1/2 khoảng cách xe máy đến M

Đổi 20m/s = 72km/h
Ta có Vtb = \(\frac{S}{t_1+t_2}=\frac{S}{\frac{S}{2.v_1}+\frac{S}{2.v_2}}=\frac{S}{\frac{S}{2}\left(\frac{1}{v_1}+\frac{1}{v_2}\right)}=\frac{1}{\frac{1}{2}\left(\frac{v_1+v_2}{v_1.v_2}\right)}=\frac{2.v_1.v_2}{v_1+v_2}=\frac{2.50.72}{50+72}=59,01\)km/h

Thời gian đi trên nửa đoạn đường đầu là:
\(t_1=\dfrac{AB}{2v_1}=\dfrac{AB}{2.50}=\dfrac{AB}{100}\left(h\right)\)
Thời gian đu trên nửa đoạn đường sau là:
\(t_2=\dfrac{AB}{2v_2}=\dfrac{AB}{2.20}=\dfrac{AB}{40}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường AB là:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{AB}{\dfrac{AB}{100}+\dfrac{AB}{40}}=\dfrac{AB}{AB\left(\dfrac{1}{100}+\dfrac{1}{40}\right)}=\dfrac{1}{\dfrac{1}{100}+\dfrac{1}{40}}=\dfrac{200}{7}\approx28,57\left(km/h\right)\)

a) Ta có: \(\left\{{}\begin{matrix}t_1=\dfrac{S_1}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{40}\left(h\right)\\t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2v_2}=\dfrac{S}{120}\left(h\right)\end{matrix}\right.\)
Vận tốc TB ô tô đi từ M đến N:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{120}}=\dfrac{S}{S\left(\dfrac{1}{40}+\dfrac{1}{120}\right)}=30\left(\dfrac{km}{h}\right)\)
b) Ta có: \(\left\{{}\begin{matrix}S_1'=t_1'.v_1=20t\left(km\right)\\S_2'=t_2'.v_2=60t\left(km\right)\end{matrix}\right.\)
Vận tốc TB ô tô đi từ N về M:
\(v_{tb}'=\dfrac{S_1'+S_2'}{t_1'+t_2'}=\dfrac{20t+60t}{2t}=40\left(\dfrac{km}{h}\right)\)
Thời gian đi và thời gian về lần lượt là:
\(t=\dfrac{S}{30}\left(h\right),t'=\dfrac{S}{40}\left(h\right)\Rightarrow t>t'\)
Vậy thời gian đi nhiều hơn thời gian về
d) Theo đề bài ta có:
\(t-t'=0,5\Rightarrow\dfrac{S}{30}-\dfrac{S}{40}=0,5\Rightarrow S\left(\dfrac{1}{30}-\dfrac{1}{40}\right)=0,5\Rightarrow S_{MN}=60\left(km\right)\)

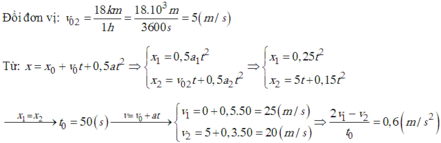

thời gian tàu đi với vận tốc V1=\(\dfrac{27}{90}\)=0,3h
thời gian tàu đi với vận tốc v2=\(\dfrac{90-27}{72}\)=0,875h
sau thời gian 0,875+0,3=1,175 h thì tàu đến B
Vtb=\(\dfrac{S_1+S_2}{\dfrac{S_1}{90}+\dfrac{S_2}{72}}\)=\(\dfrac{90}{\dfrac{27}{90}+\dfrac{63}{72}}\)~76,6km/h
hihi mình cũng không biết đúng hay sai nữa bạn sửa giùm mình nha
tại sao lại v2=90-27/72=0.875??????