Cho tam giác ABC có I là trung điểm AB, K là trung điểm AC. Trên tia đối của KI lấy điểm M sao cho KI=KM. Chứng minh rằng:
a) Tam giác AKI= tam giác CKM
b) AI // MC
c) IK // BC và IK = 1/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
1 tháng 12 2017
a)xét tam giác AKI và tam giác CKM có
KI =KM (giả thiết )
góc AKI = góc CKM ( 2 góc đối đỉ̉nh )
AK= CK ( K là trung điểm của CA )
suy ra tam giác AHI = tam giác CKM
b) tam giác AKI= tam giác CKM
suy ra góc MCK =góc KAI ( 2 GÓC TƯƠNG ƯỚNG)
mà chúng ở vị trí so le trong do AC cắt AI và MC
suy ra AI // MC
c ) MK 0 BIEI LAM
2 tháng 11 2016
Ta có hình vẽ:
a) Vì M là trung điểm của AB nên AM = BM = \(\frac{AB}{2}\)
Xét Δ AMK và Δ BMC có:
AM = BM (cmt)
AMK = BMC (đối đỉnh)
MK = MC (gt)
Do đó, Δ AMK = Δ BMC (c.g.c) (đpcm)
b) Vì N là trung điểm của AC nên AN = NC
Xét Δ ANI và Δ CNB có:
AN = NC (cmt)
ANI = CNB (đối đỉnh)
NI = NB (gt)
Do đó, Δ ANI = Δ CNB (c.g.c)
=> AI = BC (2 cạnh tương ứng) (đpcm)
c) Vì Δ AMK = Δ BMC (câu a) => AKM = MCB (2 góc tương ứng)
Mà AKM và MCB là 2 góc so le trong nên AK // BC (1)
Vì Δ ANI = Δ CNB (câu b) => IAN = NBC (2 góc tương ứng)
Mà IAN và NBC là 2 góc so le trong nên AI // BC (2)
Từ (1) và (2) => AK và AI trùng nhau hay 3 điểm I, A, K thẳng hàng (3)
Có: Δ AMK = Δ BMC (câu a) => AK = BC (2 cạnh tương ứng)
Mà AI = BC (câu b) => AK = AI (4)
Từ (3) và (4) => A là trung điểm của IK (đpcm)
8 tháng 12 2021
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
16 tháng 1 2022
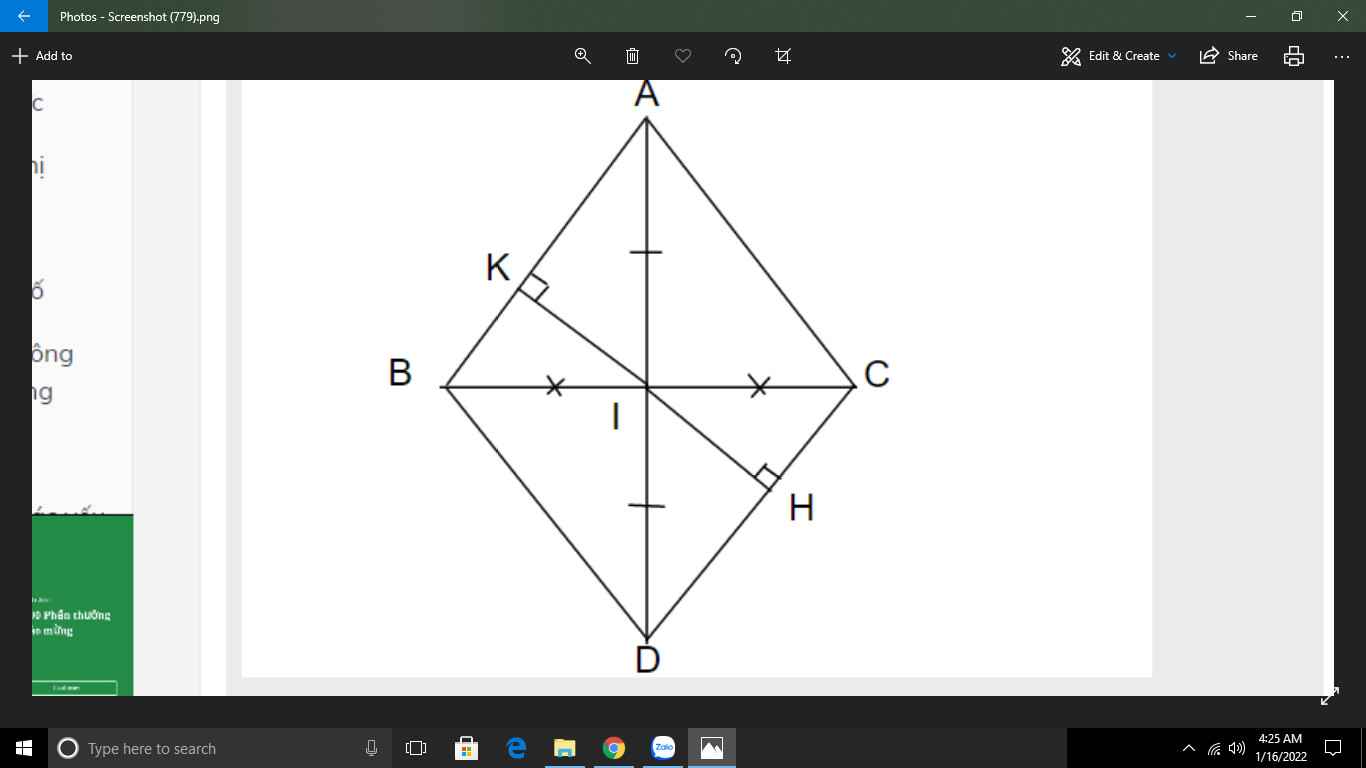
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)
6 tháng 1 2022
a: Xét ΔAGI và ΔBGC có
GA=GB
\(\widehat{AGI}=\widehat{BGC}\)
GI=GC
Do đó: ΔAGI=ΔBGC
b: Xét tứ giác ABCK có
H là trung điểm của AC
H là trung điểm của BK
Do đó: ABCK là hình bình hành
Suy ra: AK//BC và AK=BC(1)
Xét tứ giác AIBC có
G là trung điểm của AB
G là trung điểm của IC
Do đó: AIBC là hình bình hành
Suy ra: AI//BC và AI=BC(2)
Từ (1) và (2) suy ra AI=AK và I,A,K thẳng hàng
hay A là trung điểm của IK
27 tháng 1 2022
a: Xét ΔAHB và ΔAHC có
AH chung
HB=HC
AB=AC
Do đó: ΔAHB=ΔAHC
b: Xét tứ giác ABMC có
H là trung điểm của AM
H là trung điểm của BC
Do đó: ABMC là hình bình hành
Suy ra: AB//MC
20 tháng 8 2023
a: Xét ΔCBD có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
b: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>AM=1/2MC
c: Gọi giao của d với AC là E
d là trung trực của AE
=>QE vuông góc AC tại E và E là trung điểm của AC
Xét ΔCAD có
E là trung điểm của CA
EQ//DA
=>Q là trung điểm của CD
Xét ΔCBD có
M là trọng tâm
BQ là đường trung tuyến
Do đó; B,Q,M thẳng hàng
26 tháng 3 2023
1: Xét ΔCIO vuông tại Ivà ΔCHO vuông tại H có
CO chung
góc ICO=góc HCO
=>ΔCIO=ΔCHO
=>CI=CH
=>ΔCIH cân tại C
2:
Kẻ AE//BC, E thuộc IH
=>góc AEH=góc HIC=góc IHC=góc AHE
=>ΔAHE cân tại A
=>AE=AH=IK
Xét ΔAEM và ΔKIM có
góc MAE=góc MIK
AE=IK
góc AME=góc KMI
=>ΔAEM=ΔKIM
=>AM=KM
=>M là trung điểm của AK
c: Kẻ OD vuông góc AB
Xét ΔAOD vuông tại D và ΔAOH vuông tại H có
AO chung
góc OAD=góc OAH
=>ΔAOD=ΔAOH
=>AD=AH=IK
Xet ΔBOD và ΔBOI có
góc BDO=góc BIO
BO chung
góc DBO=góc IBO
=>ΔBDO=ΔBIO
=>BD=BI
BK=BI+IK=BD+AD=BA
=>ΔBKA cân tại B
=>BO vuông góc AK
Xét ΔAHO và ΔOIK có
AH=IK
OH=OI
góc AHO=góc OIK=90 độ
=>ΔAHO=ΔKIO
=>OA=OK
=>ΔOAK cân tại O
mà M là trung điểm của AK
nên OM vuông góc AK
=>B,O,M thẳng hàng
a) Xét ΔAKI và ΔCKM , ta có :
AK = KC ( k là trung điểm của AC )
IK = KM ( gt )
Góc AKI = MKC ( 2 góc đối đỉnh )
=> ΔAKI = ΔCKM (cgc )
b) Ta có : ΔAKI = ΔCKM
=> KMC = KIA ( 2 góc tương ứng )
mà góc KMC và KIA là hai góc ở vị trí so le trong
=> AI // MC
c)Ta có :
+ MC = AI ( ΔAKI = ΔCKM )
+ AI = IB ( I là trung điểm của AB )
=> MC = IB
+ MI // AI => MI // IB
Xét ΔMCI và ΔCIB , có :
MC = IB ( c/m t )
IC là cạnh chung
Góc MCI = CIB ( 2 góc so le trong , MC // IB )
=> ΔMCI = ΔBIC ( cgc )
=> Góc MIC = BCI ( 2 góc tương ứng )
mà MIC và BCI là góc góc ở vị trí so le trong
=> IK // BC
Ta có : IK = \(\frac{MI}{2}\) => IK = \(\frac{1}{2}MI\)
Mà BC = MI ( ΔMCI = ΔBIC )
=> IK = \(\frac{BC}{2}\Rightarrow IK=\frac{1}{2}BC\)
Thầy @phynit có thể giải giúp em không ạ?