Trong hình 1, biết ∠D1 = 700 , ∠C2 = 110 , c⊥a. a/ Chứng minh: a//b b/ Chứng minh: c⊥b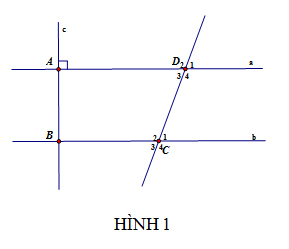
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
2
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
14 tháng 8 2023
a) Ta thấy:
\(\widehat{BED}+\widehat{EBC}=180^o\)
Mà hai góc này ở vị trí trong cùng phía
\(\Rightarrow DE//BC\)
b) Mà: DE//BC
\(\Rightarrow\widehat{EDC}+\widehat{BCD}=180^o\)(hai góc trong cùng phía)
\(\Rightarrow\widehat{EDC}=180^o-\widehat{BCD}=180^o-40^o=140^o\)
Ta lại có:
\(\widehat{EDC}\) đối đỉnh \(\widehat{xDC}\)
\(\Rightarrow\widehat{xDC}=\widehat{EDC}=140^o\)
KV
14 tháng 8 2023
a) Ta có:
∠BED + ∠EBC = 110⁰ + 70⁰ = 180⁰
Mà ∠BED và ∠EBC là hai góc trong cùng phía
⇒ DE // BC
b) Do DE // BC
⇒ ∠EDC + ∠DCB = 180⁰ (hai góc trong cùng phía)
⇒ ∠EDC = 180⁰ - ∠DCB
= 180⁰ - 40⁰
= 140⁰
Do DE // BC
⇒ ∠xDC = ∠DCB = 40⁰ (so le trong)
24 tháng 12 2023
a: Ta có: AC\(\perp\)AB
BD\(\perp\)AB
Do đó: AC//BD
b: bạn vẽ lại hình nha bạn
15 tháng 10 2017
a) Ta có: \(\left\{{}\begin{matrix}a\perp c\\b\perp c\end{matrix}\right.\Rightarrow a//b\)
b) Ta có:
\(\widehat{D2}=\widehat{D1}=130^o\)( đối đỉnh)
\(\Rightarrow\widehat{D2}=130^0\)
\(\widehat{C2}+\widehat{D1}=180^0\)( trong cùng phía vì a//b)
\(\widehat{C2}+130^0=180^0\\ \widehat{C2}=180^0-130^0\\ \widehat{C2}=50^0\\ \Rightarrow\widehat{C2}=50^0\)
Vì trong hình không có góc C1 nên mình không tính được bạn nhé
15 tháng 10 2017
Ta có: \(\widehat{C1}=\widehat{D1}=130^0\)( sole trong vì a//b)
\(\Rightarrow\widehat{C1}=130^0\)
đây nha bạn 
18 tháng 10 2016
trc hết D1= 70O
a) D1 = D3= 70 (đối đỉnh)
C2 + D3 = 110+70 = 180 ( 2 góc này ở
vị trí trong cùng phía) nên a//b
b) theo a) có a//b
mà c vuông góc với a => c vuong goc voi b
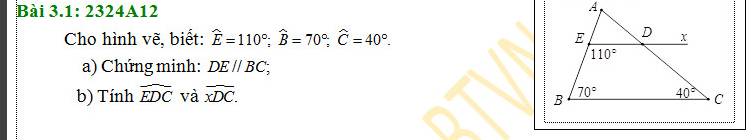
Ta có: \(\widehat{C_1}\)+\(\widehat{C_2}\)=1800 (kề bù)
hay \(\widehat{C_1}\)+1100 = 1800
=> \(\widehat{C_1}\)= 1800 - 1100 = 700
Ta có: \(\widehat{C_1}\)=\(\widehat{D_1}\)=700
Mà \(\widehat{C_1}\); \(\widehat{D_1}\) :đồng vị
=> a // b
Ta có: a // b; a\(\perp\)c
=> b \(\perp\) c hay c \(\perp\)b (đpcm)
C1 + C2 = 1800 (2 góc kề bù)
C1 + 1100 = 1800
C1 = 1800 - 1100
C1 = 700
mà D1 = 700
=> C1 = D1
mà 2 góc này ở vị trí đồng vị
=> a // b
mà c _I_ a
=> c _I_ b