Câu 2: Chọn khẳng định đúng.
A. Hai vectơ cùng phương thì bằng nhau.
B. Hai vectơ ngược hướng thì có độ dài không bằng nhau.
C. Hai vectơ cùng phương và cùng độ dài thì bằng nhau.
D. Hai vectơ cùng hướng và cùng độ dài thì bằng nhau.
Câu 3: Mệnh đề nào sau đây đúng?
A. Hai vectơ cùng phương với vectơ thứ ba thì cùng phương.
B. Mọi vectơ đều có độ dài lớn hơn 0.
C. Một vectơ có điểm đầu và điểm cuối phân biệt thì không là vectơ - không. D. Hai vectơ bằng nhau khi chúng cùng phương và cùng độ dài.
Câu 4: Gọi M, N lần lượt là trung điểm của các cạnh AB, AC của tam giác đều ABC. Đẳng thức nào sau đây đúng?
A. MA MB . B. AB AC . C. MN BC . D. BC MN 2 .
Câu 5: Cho lục giác đều ABCDEF tâm O. Số các vectơ bằng OC có điểm đầu và điểm cuối là các đỉnh của lục giác là A. 2. B. 3. C. 4. D. 6. Câu 6: Cho bốn điểm A, B, C, D tùy ý. Nếu AB CD thì
A. AC DB . B. CD AD . C. AC BD . D. CA BD .
Câu 7: Cho ba điểm A, B, C không thẳng hàng, M là điểm bất kỳ. Mệnh đề nào sau đây đúng?
A. MA MB với mọi M.
B. Có một điểm M sao cho MA MB MC .
C. MA MB MC với mọi M.
D. Có một điểm M sao cho MA MB .



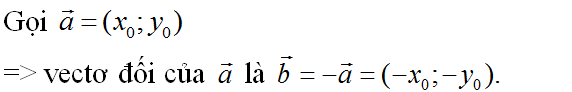

2D
3C
4,5,6 đề lỗi