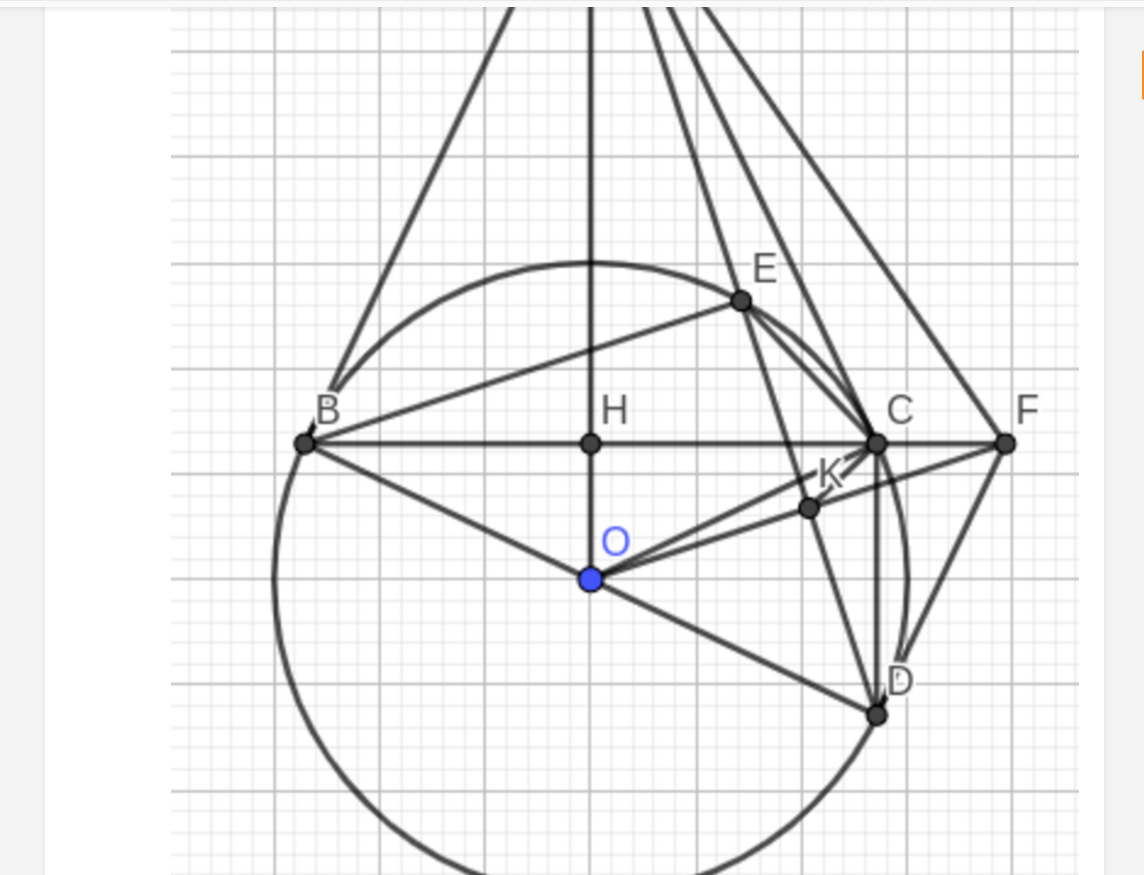
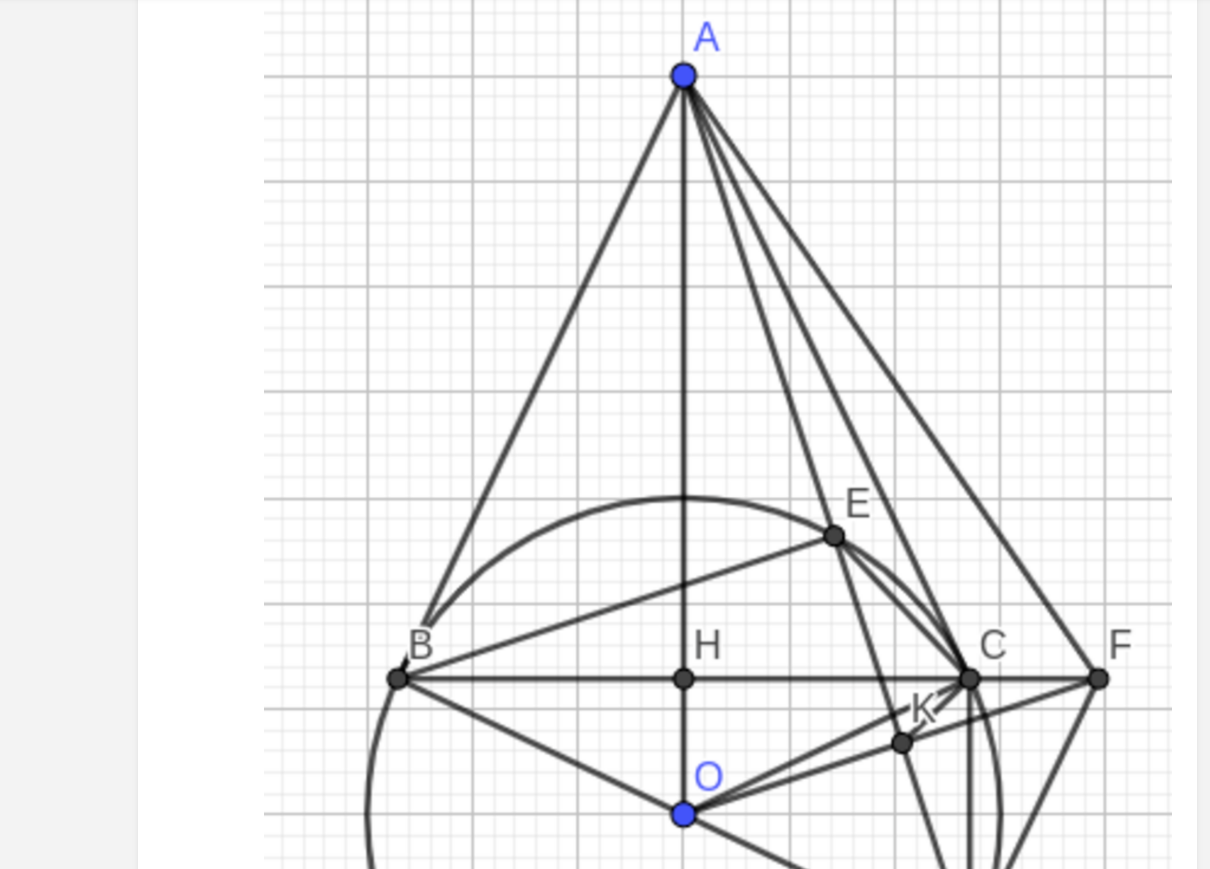
Cho (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC. Từ B vẽ đường kính BD của (O), đường thẳng AD cắt (O) tại E (khác D). Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh DF là tiếp tuyến của (O).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2022
a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét ΔAEC và ΔACD có
gó ACE=góc ADC
góc EAC chung
Do đo: ΔAEC đồng dạng với ΔACD
=>AE/AC=AC/AD
=>AC^2=AE*AD
15 tháng 12 2022
a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét ΔAEC và ΔACD có
gó ACE=góc ADC
góc EAC chung
Do đo: ΔAEC đồng dạng với ΔACD
=>AE/AC=AC/AD
=>AC^2=AE*AD
2 tháng 1
a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>A,B,O,C cùng nằm trên 1 đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔABD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\)(3)
=>\(AE\cdot AD=AC^2\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
góc EAH chung
Do đó: ΔAEH đồng dạng với ΔAOD
=>\(\widehat{AHE}=\widehat{ADO}\)
c: Ta có: ΔOED cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)ED tại K
Xét ΔBOA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\)
Xét ΔOKA vuông tại K và ΔOHF vuông tại H có
\(\widehat{KOA}\) chung
Do đó: ΔOKA đồng dạng với ΔOHF
=>\(\dfrac{OK}{OH}=\dfrac{OA}{OF}\)
=>\(OK\cdot OF=OA\cdot OH\)
=>\(OK\cdot OF=R^2=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
Xét ΔOKD và ΔODF có
\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
góc KOD chung
Do đó: ΔOKD đồng dạng với ΔODF
=>\(\widehat{OKD}=\widehat{ODF}\)
=>\(\widehat{ODF}=90^0\)
=>FD là tiếp tuyến của (O)
BC
30 tháng 12 2021
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC
23 tháng 2 2021
a) Xét tứ giác OBAC có
\(\widehat{OBA}\) và \(\widehat{OCA}\) là hai góc đối
\(\widehat{OBA}+\widehat{OCA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OBAC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
23 tháng 6 2023
a: ΔODE cân tại O
mà OK là trung tuyến
nên OK vuông góc DE
góc OKA=góc OBA=góc OCA=90 độ
=>O,K,C,A,B cùng thuộc 1 đường tròn
b: Xét ΔACE và ΔADC có
góc ACE=góc ADC
góc CAE chung
=>ΔACE đồng dạng với ΔADC
=>AC/AD=AE/AC
=>AC^2=AD*AE
c: Xét ΔOKA vuông tại K và ΔOHF vuông tại H có
góc O chung
=>ΔOKA đồng dạng với ΔOHF
=>OK/OH=OA/OF
=>OK*OF=OH*OA=OE^2=OD^2
=>FD là tiếp tuyến của (O)
LA
28 tháng 12 2016
Dễ thấy: A,B,O,K,CA,B,O,K,C nằm trên đường tròn đường kính OAOA .
Ta có: AE.AD=AB2=AH.AO⇒E,D,H,OAE.AD=AB2=AH.AO⇒E,D,H,O cùng thuộc 1 đường tròn
Mặt khác: A,E,B,HA,E,B,H cùng thuộc đường tròn đường kính ABAB nên ˆEHF=ˆBAD=ˆEBD=ˆEOFEHF^=BAD^=EBD^=EOF^
Suy ra: E,H,O,FE,H,O,F đồng viên. Suy ra: E,H,O,F,DE,H,O,F,D cùng thuộc đường tròn đường kính OFOF.
Gọi JJ là giao điểm của ININ và ADAD.
Xét 2 tam giác: ΔIHJΔIHJ và ΔFHDΔFHD
Ta có: ˆJIH=ˆAIJJIH^=AIJ^ (t/c đối xứng) =ˆABC=ˆDFH=ABC^=DFH^
Mặt khác:ˆIHJ=ˆIAJIHJ^=IAJ^(t/c đối xứng) =ˆEOF=ˆDHF=EOF^=DHF^
Suy ra:ΔIHJΔIHJ và ΔFHDΔFHD đồng dạng nên JHHD=IHFHJHHD=IHFH
Mà IBFNIBFN là hình bình hành nên NF=IB=IHNF=IB=IH hay JHHD=NFFHJHHD=NFFH
Mà ˆJHD=ˆNFHJHD^=NFH^ (dùng cộng góc, góc nội tiếp,...)
nên ΔJHDΔJHD và ΔNFHΔNFH đồng dạng nên JHDNJHDN nội tiếp
Ta suy ra:ˆNHD=ˆNJD=ˆHDFNHD^=NJD^=HDF^ nên suy ra: NH=NDNH=ND
Mà NH=NANH=NA (t/c đối xứng) nên NA=NDNA=ND(đ.p.c.m)