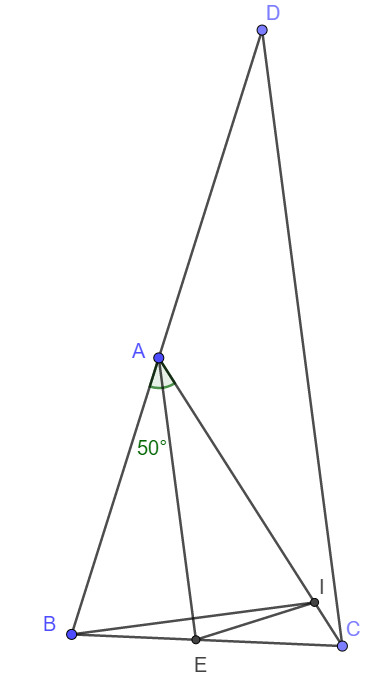
Cho tam giác ABC (AB>AC) và góc A=50o. Tia phân giác của góc A cắt BC tại E. Trên AC lấy điểm I sao cho AI=AC. Qua C kẻ đường thẳng song song với AE cắt BA tại D. Chứng minh:
a) EB=EI
b)BI=CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2021
a) Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABD=ΔHBD(cạnh huyền-góc nhọn)
Suy ra: BA=BH(hai cạnh tương ứng)
CH
Cô Hoàng Huyền
Admin
VIP
12 tháng 3 2018
a) Xét tam giác ABE và tam giác AIE có:
Cạnh AE chung
AB = AI
\(\widehat{BAE}=\widehat{IAE}\)
\(\Rightarrow\Delta ABE=\Delta AIE\left(g-c-g\right)\)
\(\Rightarrow EB=EI\) (Hai cạnh tương ứng)
b) Xét tam giác ABI cân tại A nên có tia phân giác AE đồng thời là đường cao. Vậy nên \(AE\perp BI\)
Lại có AE // DC nên \(BI\perp CD.\)
12 tháng 12 2021
Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC
