Ai giúp mình với, bài 44, 45 sgk 7 tập 1 trang 26
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


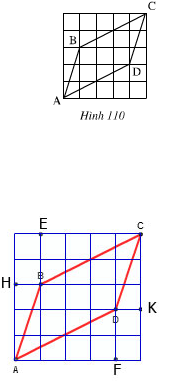
+ ΔAHB và ΔCKD có
HB = KD (=1)
góc AHB = góc CKD(=90º)
AH = CK (=3).
⇒ ΔAHB = ΔCKD(c.g.c)
⇒AB = CD (hai cạnh tương ứng)
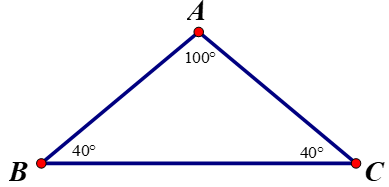
+ ΔCEB và ΔAFD có
BE = DF (=2)
góc BEC = góc DFA (=90º)
CE = AF (=4).
⇒ ΔCEB = ΔAFD ( c.g.c)
⇒ BC = AD (hai cạnh tương ứng)
b) ΔABD và ΔCDB có
AB = CD
AD = BC
BD cạnh chung
⇒ ΔABD = ΔCDB (c.c.c)
⇒ góc ABD = góc CDB (hai góc tương ứng)
Vậy AB // CD ( hai gó so le trong bằng nhau )
k minh nha
(hình hơi xấu, thông cảm nha)
a) Xét \(\Delta AEB\)và \(\Delta DFC\) có:
AE = DF
\(\widehat{AEB}=\widehat{DFC}=90^o\)
BE = CF
Do đó: \(\Delta AEB=\Delta DFC\) (c.g.c)
Suy ra: AB = DC (đpcm)
Xét \(\Delta BMC\) và \(\Delta DNA\) có:
MC = NA
\(\widehat{BMC}=\widehat{DNA}=90^o\)
BM = DN
Do đó: \(\Delta BMC=\Delta DNA\)
Suy ra: BC = AD (đpcm)
b) Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB = CD (câu a)
BC = AD (câu a)
BD là cạnh chung
Do đó: \(\Delta ABD=\Delta CDB\) (c.c.c)
Suy ra: \(\widehat{ABD}=\widehat{CDB}\) (so le trong)
=> AB // CD (đpcm)



bạn hay xem video bài giảng trong link này nha
https://www.youtube.com/watch?v=wBWTiEHKnqM

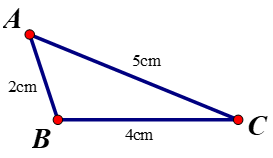
Dựa vào hình vẽ, ta có:
Góc đối diện cạnh BC là Â
Góc đối diện cạnh AC là B̂
Góc đối diện cạnh AB là Ĉ
Mà: Trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn
Tam giác ABC có AB = 2cm, BC = 4cm, AC = 5cm ⇒ AB < BC < CA ⇒ Ĉ < Â < B̂.
2)heo định lý tổng ba góc trong tam giác ABC, ta có:
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Kiến thức áp dụng
+ Định lí 2: Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
+ Định lý tổng ba góc trong tam giác: Trong một tam giác, tổng ba góc bằng 180º.
3 a) Trong tam giác ABC có góc A là góc tù nên cạnh đối diện với góc A là cạnh lớn nhất.
Cạnh đối diện với góc A là BC nên suy ra cạnh BC lớn nhất.
b) Tam giác ABC là tam giác tù vì có 1 góc A tù.
Áp dụng định lý tổng ba góc trong tam giác ABC ta có
4) Trong một tam giác ta luôn có:
+ Góc đối diện với cạnh lớn hơn là góc lớn hơn
⇒ góc đối diện với cạnh nhỏ nhất là góc nhỏ nhất.
+ Góc nhỏ nhất luôn là góc nhọn.
(Giả sử tồn tại tam giác có góc nhỏ nhất không phải góc nhọn
⇒ Góc nhỏ nhất ≥ 90º ⇒ cả ba góc ≥ 90º ⇒ tổng ba góc trong tam giác ≥ 90º.3 = 270º.
5) + Trong ∆BCD có góc C tù (gt) nên góc C lớn nhất ⇒ BD lớn nhất (vì BD là cạnh đối diện với góc C) ⇒ BD > CD (1).
+ Áp dụng định lý góc ngoài trong tam giác BCD ta có :
nên góc ABD cũng là góc tù.
Trong ∆ABD có góc B tù (cmt) nên góc B lớn nhất ⇒ AD lớn nhất (vì AD là cạnh đối diện với góc B) ⇒ AD > BD
(2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy Hạnh đi xa nhất, Trang đi gần nhất.
6)Vì D nằm giữa A và C (giả thiết)
⇒ AC = AD + DC = AD + BC (DC = BC theo đề bài)
⇒ AC > BC
Mà trong tam giác ABC :
Góc đối diện cạnh AC là góc B
Góc đối diện cạnh BC là góc A
Ta lại có: AC > BC (cmt)
⇒ B̂ > Â (theo định lí 1)
Hay  < B̂.
Vậy kết luận c) là đúng.
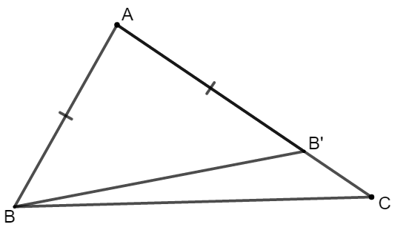
7)
a) Trên tia AC, ta có : AC > AB mà AB = AB’ ⇒ AC > AB’ ⇒ B’ nằm giữa A và C.
⇒ tia B’B nằm giữa hai tia BA và BC.
b) ∆ABB’ có AB = AB’ nên ∆ABB’ cân tại A.
c) Vì góc AB'B là góc ngoài tại B’ của ∆BB’C

bạn cứ gõ lên goole bài 45 sgk tr99 toán 7 tập 1 sẽ có . tick nha

Tham khảo:
Câu so sánh thú vị: “ Dượng Hương Thư như một pho tượng đúc đồng… hiệp sĩ của Trường Sơn oai linh hùng vĩ.
-> Vẻ đẹp rắn rỏi, kiên cường của con người trước khó khăn, thử thách.

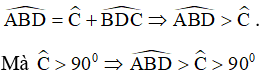
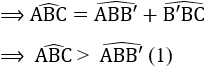
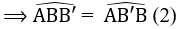
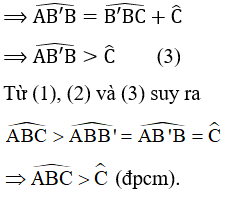
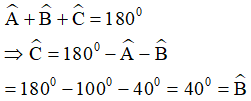
Bài 44:
a, 1,2 : 3,24 = \(\frac{1,2}{3,24}=\frac{120}{324}=\frac{10}{27}\)
b, \(2\frac{1}{5}:\frac{3}{4}=3\frac{41}{45}=\frac{176}{45}\)
c,\(\frac{2}{7}:0,42=\frac{\frac{2}{7}}{0,42}=\frac{2}{7}.\frac{100}{42}=\frac{100}{147}\)
vào đây nè:Chuyên trang lý thuyết tổng hợp các môn THPT bài nào cũng có