câu 6. cho tam giác ABC vuông tại A, đường cao AH. Gọi D là điểm đối xứng với H qua AC, gọi E là điểm đối xứng với H qua AB. chứng minh
a/ D đối xứng với E qua A
b/ tam giác DHE vuông
c/ tứ giác BDEC là hình thang vuông
d/ BC= BD+CE
cố giúp mình nhé. cần gấp. không cần vẽ hình đâu, giải thui, mình vẽ được hình rồi


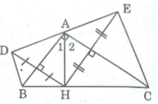
a: Ta có: H và E đối xứng với nhau qua AB
nên AB là đường trung trực của HE
=>AH=AE
=>ΔAEH cân tại A
mà AB là đường trung tuyến
nên AB là tia phân giác của góc HAE(1)
Ta có: H và D đối xứng nhau qua AC
nên AC là đường trung trực của HD
=>AH=AD
=>ΔAHD cân tại A
mà AC là đường cao
nên AC là tia phân giác của góc HAD(2)
Từ (1) và (2) suy ra \(\widehat{DAE}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)=2\cdot90^0=180^0\)
=>D,A,E thẳng hàng
mà AD=AE
nên A là trung điểm của DE
b: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
Do đó: ΔDHE vuông tại H