|x| + 1=X2 +m có nghiệm duy nhất khi và chỉ khi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 4 2018
x + 1 = x 2 + m ⇔ m = f x = − x 2 + x + 1 k h i x ≥ 0 − x 2 − x + 1 k h i x < 0
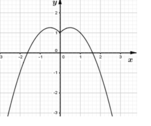
Biểu diễn đồ thị hàm số f(x) lên hệ trục tọa độ như hình vẽ bên trên:
+ Vẽ đồ thị hàm số y = - x 2 + x + 1
+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.
+ Xóa bỏ phần bên trái trục tung trước đó đi.
Dựa vào đồ thị ta suy ra không tồn tại m để phương trình m = f x có duy nhất 1 nghiệm.
Đáp án cần chọn là: D
CM
3 tháng 1 2017
Chọn C.
Xét phương trình: x 2 - (m + 1)x + 1 = 0
Ta có: Δ = (m + 1 ) 2 - 4.1.1 = m 2 - 2m + 1 - 4 = m 2 - 2m - 3
Phương trình x 2 - (m + 1)x + 1 = 0 có nghiệm
⇔ Δ ≥ 0 ⇔
m
2
- 2m - 3 ≥ 0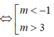 
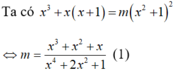
CM
2 tháng 10 2017
Xét hàm số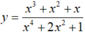 
xác định trên R.
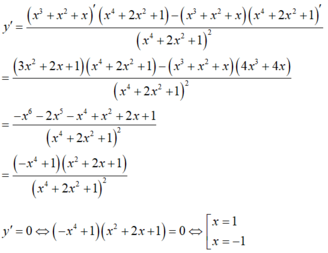
Bảng biến thiên
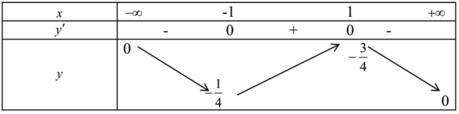
Phương trình (1) có nghiệm thực khi đường thẳng y= m cắt đồ thị hàm số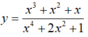 
Khi và chỉ khi -1/4 ≤ m≤ 3/4
Chọn D.
AT
11 tháng 6 2021
ý 1: Để pt (1) có 1 nghiệm duy nhất thì \(\Delta=0\)
\(\Delta=\left(-5\right)^2-4m+8=-4m+33\)
\(\Rightarrow33-4m=0\Rightarrow m=\dfrac{33}{4}\)
ý 2: Khi \(m=4\Rightarrow x^2-5x+2=0\)
\(\Delta=\left(-5\right)^2-8=17\Rightarrow\left[{}\begin{matrix}x=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{5-\sqrt{17}}{2}\\x=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{5+\sqrt{17}}{2}\end{matrix}\right.\)
Vậy...
CM
28 tháng 2 2017
Đáp án B
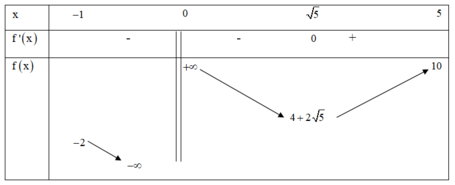
Phương pháp: Số nghiệm của phương trình f(x) = m là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m song song với trục hoành.
Cách giải: Dựa vào bảng biến thiên ta thất để phương trình f(x) = m có nghiệm duy nhất thì đường thẳng y = m cắt đồ thị hàm số y = f(x) tại 1 điểm duy nhất
→ m ∈ - ∞ ; - 2 ∪ { 4 + 2 5 } ∪ [ 10 + ∞ )
CM
17 tháng 5 2018
Đáp án B
Dựa trên BBT ta thấy PT có nghiệm duy nhất ⇔ − 3 < m < 3
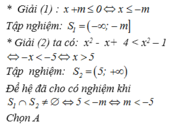
Ta có \(m=1-x^2\le1\) . Vậy ta xét các khoảng giá trị của m :
+ Nếu m = 1 thì \(x=0\) thỏa mãn nghiệm duy nhất.
+ Nếu \(0\le m< 1\) thì \(1-m>0\) , vậy lúc đó pt có hai nghiệm
\(x=\pm\sqrt{1-m}\)
+ Nếu \(m=0\) thì \(x=\pm1\)
+ Nếu \(m< 0\) thì \(x^2=1+m\Leftrightarrow x=\pm\sqrt{1+m}\) luôn có hai nghiệm.
Vậy m = 1 thỏa mãn đề bài.