cho 2 số a,b thoã mãn\(\frac{a}{b}=\frac{-4}{5}\)và a2+2b2=16,5
giá trị lớn nhất của a+b là :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
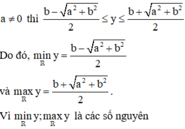
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
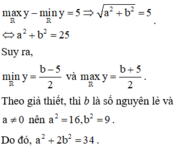

\(2a^2+\frac{1}{a^2}+\frac{b^2}{4}=4\Leftrightarrow\left(a^2+\frac{1}{a^2}-2\right)+\left(a^2+\frac{b^2}{4}-ab\right)=4-ab-2\)
\(\Leftrightarrow\left(a-\frac{1}{a}\right)^2+\left(a-\frac{b}{2}\right)^2=2-ab\)
\(VF=2-ab=\left(a-\frac{1}{a}\right)^2+\left(b-\frac{b}{2}\right)^2\ge0\)
Hay \(ab\le2\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}a=\frac{1}{a}\\b=\frac{b}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\left(a;b\right)=\left(1;\frac{1}{2}\right)\\\left(a;b\right)=\left(-1;-\frac{1}{2}\right)\end{cases}}\)

a3+b3+c3=3abc
<=>(a+b)3-3ab(a+b)-3abc+c3=0
<=>(a+b+c)[(a+b)2-(a+b)c+c2]-3ab.(a+b+c)=0
<=>(a+b+c)(a2+b2+c2-ab-bc-ac)=0
<=>(a+b+c)(2a2+2b2+2c2-2ab-2bc-2ac)=0
<=>(a+b+c)[(a-b)2+(b-c)2+(c-a)2]=0
<=>a+b+c=0 [(a-b)2+(b-c)2+(c-a)2 khác 0]
=>a2+b2-c2=-2ab;b2+c2-a2=-2bc;c2+a2-b2=-2ac
Suy ra : P=\(-\left(\dfrac{1}{2ab}+\dfrac{1}{2bc}+\dfrac{1}{2ac}\right)=-\dfrac{a+b+c}{2abc}=0\)
a/b=-4/5
nên a/-4=b/5
Đặt a/-4=b/5=k
=>a=-4k; b=5k
\(a^2+2b^2=16.5\)
\(\Leftrightarrow16k^2+50k^2=16.5\)
\(\Leftrightarrow k^2=\dfrac{1}{4}\)
Trường hợp 1: k=1/2
=>a=-2; b=5/2
=>a+b=1/2
Trường hợp 2: k=-1/2
=>a=2; b=-5/2
=>a+b=-1/2
Vậy: Giá trị lớn nhất của a+b là 1/2