Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét tam giác ABD và tam giác EBD có:
+ ^ABD = ^EBD (do BD là phân giác ^B).
+ BD chung.
+ AB = BE (gt).
=> Tam giác ABD = Tam giác EBD (c - g - c).
=> DA = DE (2 cạnh tương ứng).
b) Tam giác ABD = Tam giác EBD (cmt).
=> ^BAD = ^BED (2 góc tương ứng).
Mà ^BAD = 90o (gt).
=> ^BED = 90o.
a) xét ΔABD và ΔEBD có:
BA = BE (GT)
∠ABD=∠EBD( BD là tia phân giác ∠ABE)
BD chung⇒ΔABD=ΔEBD(ch-cgv)
⇒AD=ED (2 cạnh tương ứng)
b)Vì ΔABD=ΔEBD(CMT)
⇒∠BAD=∠BED(2 góc tương ứng)
Mà ∠BAD= 90 độ
⇒∠BED = 90 độ
a) Xét ΔADB và ΔEDB có:
BA = BE ( giả thiết )
Góc ABD = EBD ( BD là tia phân giác của góc ABE )
BD cạnh chung.
=> ΔADB = ΔEDB ( c.g.c )
=> DA = DE ( 2 cạnh tương ứng )
b) Vì ΔADB = ΔEDB nên góc DAB = DEB = 90 độ ( 2 góc tương ứng).
Xét ΔABD và ΔEBD, ta có:
AB = BE (gt)
∠(ABD) = ∠(DBE) (vì BD là tia phân giác)
BC cạnh chung
Suy ra: ΔABD = ΔEBD(c.g.c)
⇒ DA = DE (hai cạnh tương ứng)
Bài làm
a) Xét tam giác ABD và tam giác EBD
Ta có: BA = BE ( giả thiết )
\(\widehat{ABD}=\widehat{DBE}\)( BD là tia phân giác của góc ABC )
BD là cạnh chung
=> Tam giác ABD = tam giác EBD ( c.g.c )
=> DA = DE ( hai cạnh tương ứng )
Vậy DA = DE
b) Vì tam giác ABD = tam giác EBD
=> Góc BAD = góc BED ( hai góc tương ứng )
Mà góc BAD = 90o
=> BED = 90o
Vậy góc BED = 90o
Câu c) lỗi.
# Chúc bạn học tốt #
a,xét tam giac ABD và tam giac EBD có
BD chung
góc ABD = góc DBE(vì BDlà phân giác của góc ABE)
BA=BE(gt)
Do đó tam giác ABD bằng tam giác EBD(c.g.c)
suy ra DA=DE(2 cạnh tương ứng)
b,vì tam giac ABD=tam giác DBE=>góc a bằng góc BED
mà góc A=90 độ=>Góc BED=90độ
a/ Xét tam giác ABD và tam giác EBD có:
- Cạnh BD chung
- Góc ABD = góc DBE (vì BD là tia phân giác của góc ABE)
- BA = BE (gt)
Do đó tam giác ABD = tam giác EBD (c.g.c)
Suy ra DA = DE (2 cạnh tương ứng)
b/ Từ tam giác ABD = tam giác EBD => Góc A = góc BED (2 góc tương ứng)
Mà góc A = 90o nên góc EBD = 90o
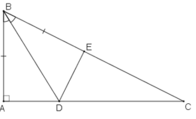
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
AD=ED
AF=EC
Do đó: ΔADF=ΔEDC
Suy ra: \(\widehat{ADF}=\widehat{EDC}\)
=>\(\widehat{ADF}+\widehat{ADE}=180^0\)
=>E,F,D thẳng hàng