Giá trị nhỏ nhất của là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Để A là phân số thì 3n+3<>0
hay n<>-1
b: Để A là số nguyên thì \(4n⋮n+1\)
\(\Leftrightarrow n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(n\in\left\{0;-2;1;-3;3;-5\right\}\)

Chọn A.
Giả sử các giá trị của mẫu số liệu là a; b; c; d với 0 < a < b < c < d và a; b; c;d là số tự nhiên.
+ Ta có 
Mà số trung bình là 6 nên a + b + c + d = 24
Suy ra a + d = 14
+ Ta có 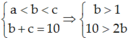 hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
hay 1 < b < 5 mà b là số tự nhiên nên b = 2; 3; 4
+ Nếu b = 2 thì c = 8, mà 0 < a < b; a là số tự nhiên nên a = 1 và d = 13
Khi đó các giá trị của mẫu số liệu là 1; 2; 8; 13
+ Nếu b = 3 thì c = 7, mà 0 < a < b; a số tự nhiên nên có 2 khả năng xảy ra: a = 1 ; d = 13 hoặc a = 2 ; d = 12
Khi đó có hai mẫu số liệu thỏa đề bài có giá trị là 1;3;7;13 và 2;3;7;12
+ Nếu b = 4 thì c = 6, mà 0 < a < b; a là số tự nhiên nên có 3 khả năng xảy ra:
a = 1; d = 13 hoặc a = 2 ; d = 12 hoặc a = 3 ; d = 11
Khi đó có ba mẫu số liệu thỏa đề bài có giá trị là 1;4;6;13 hoặc 2;4;6;12 hoặc 3;4;6;11
Suy ra với mẫu số liệu có các giá trị là 3;4;6;11 thì hiệu của giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đạt giá trị nhỏ nhất.

Đáp án D
Ta có:
− 1 ≤ sin x ≤ 1 ⇔ 5 ≥ − 5 sin x ≥ − 5 ⇔ 8 ≥ 3 − 5 sin x ≥ − 2
⇒ 0 ≤ 3 − 5 sin x 2018 ≤ 8 2018 = 2 6054

Chọn C
Tập xác định của hàm số: D = [-2;2]
Ta có 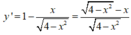
![]()
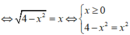
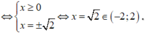
Ta lại có ![]()
Từ đó suy ra ![]()
Vậy ![]()

Chọn C.
Tập xác định của hàm số ![]()
Cách 1: Bấm máy tính. Với máy 580vn chọn start:-2, end: 2, step: 2/9 có: ![]()
thử thấy phương án C gần nhất với kết quả này nên ta chọn C.
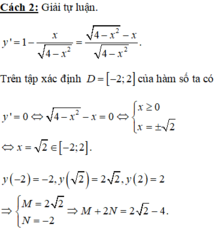


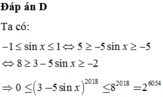
P = x2 - 2x + y2 + 6y + 19
P = x2 - x - x + 1 + y2 + 3y + 3y + 9 + 9
P = x.(x - 1) - (x - 1) + y(y + 3) + 3(y + 3) + 9
P = (x - 1)2 + (y + 3)2 + 9
Có: \(\begin{cases}\left(x-1\right)^2\ge0\\\left(y+3\right)^2\ge0\end{cases}\)\(\forall x;y\)
Do đó, \(P=\left(x-1\right)^2+\left(y+3\right)^2+9\ge9\forall x;y\)
Dấu "=" xảy ra khi \(\begin{cases}\left(x-1\right)^2=0\\\left(y+3\right)^2=0\end{cases}\)\(\Rightarrow\begin{cases}x-1=0\\y+3=0\end{cases}\)\(\Rightarrow\begin{cases}x=1\\y=-3\end{cases}\)
Vậy GTNN của P là 9 khi x = 1; y = -3