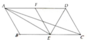
Cho hình bình hành ABCD có BC=2AB và góc A= 60 độ. Gọi E, F theo thứ tjw là trung điểm của VC và AD
a) Tứ giác ECDF là hình gì ?
b) Tứ giác ABED là hình gì ?
c) Tính góc AED
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 12 2021
a: Xét tứ giác ECDF có
EC//DF
EC=DF
Do đó: ECDF là hình bình hành
mà EC=CD
nên ECDF là hình thoi
HH
13 tháng 3 2020
a, Ta có :
EC // FD
\(EC=FD=\frac{4}{2}BC=\frac{1}{2}AD\)
=> ECDF là hình bình hành
\(EF=AB=\frac{1}{2}BC\)
=> ECDF là hình thoi
b, \(\widehat{A} =60^o\)
\(\Rightarrow D=120^o\)
\(\Rightarrow\widehat{EDF}=120^o:2=60^o\)
Mà BE // AD
==> BEDA là hình thang cân
c, Xét tam giác AFE : AF = EF --- > góc AFE
BEFA là hình thoi
==> AE là tia phân giác của \(\widehat{BAE}\Rightarrow\widehat{EAF}=30^o\)
Mà EDA = 60o
=> Trong tam giác EAD = 180o = \(\widehat{EAF}+\widehat{ADE}+\widehat{EAD}\)
\(=30^o+60^o+\widehat{EAD}\)
\(\Rightarrow\widehat{AED}=60^o\)
24 tháng 7 2023
a: Xét tứ giác ECDF có
EC//DF
EC=DF
EC=CD
=>ECDF là hình thoi
b: Xét ΔCED có CE=CD và góc C=60 độ
nên ΔCED đều
=>góc CED=60 độ
=>góc BED=120 độ
=>góc BED=góc B
Xét tứ giác ABED có
BE//AD
góc ABE=góc BED
=>ABED là hình thang cân
c: Xét ΔBAD có
BF là trung tuyến
BF=AD/2
=>ΔBAD vuông tại B
=>góc ABD=90 độ
=>góc MBD=90 độ
Xét tứ giác BMCD có
BM//CD
BM=CD
góc MBD=90 độ
=>BMCD là hình chữ nhật
d: BMCD là hình bình hành
=>BC cắt MD tại trung điểm của mỗi đường
=>M,E,D thẳng hàng
CM
23 tháng 11 2018
a) Ta sẽ có FD//EC và FD = EC = 0.5 AD Þ ECDF là hình bình hành.
Mà A B 1 2 B C
Þ AB = BE = EF = EC
Þ CDFE là hình thoi.
b) Tứ giác ABED là hình thang cân vì BE//AD và B A D ^ = A D E ^ = 60 0
c) Ta có E F = C D = A B = 1 2 C D = 1 2 A D , F là trung điểm AD Þ A E D ^ = 90 0
ở dòng thứ 2 VC ở đâu ra vậy bạn
bạn cũng cung cự giải hả. rất hân hạnh được làm quen