Rút gọn hoặc tính nếu có thể:(Mọi người làm giúp mình với mình cần gấp 9h30 tối nay phải nạp ;-;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 8 2023
\(2^4.5-\left[31-9^2\right]=16.5-\left(31-81\right)=80-\left(-50\right)=130\)
23 tháng 8 2023
\(2^4\).5-[1.31-(13-4)^2]
=16.5-[1.31-81]
=16.5-[31-81]
=16.5-(-50)
=80-(-50)
=130
A
2 tháng 1 2021
- Vì sau khi ngâm rau vào các dung dịch muối (môi trường ưu trương) để tế bào VSV bị co nguyên sinh, làm chúng không phân hia được, hoặc ngâm vào thuốc tím (hợp chất oxi hoá mạnh) à tiêu diệt vi khuẩn
20 tháng 8 2021
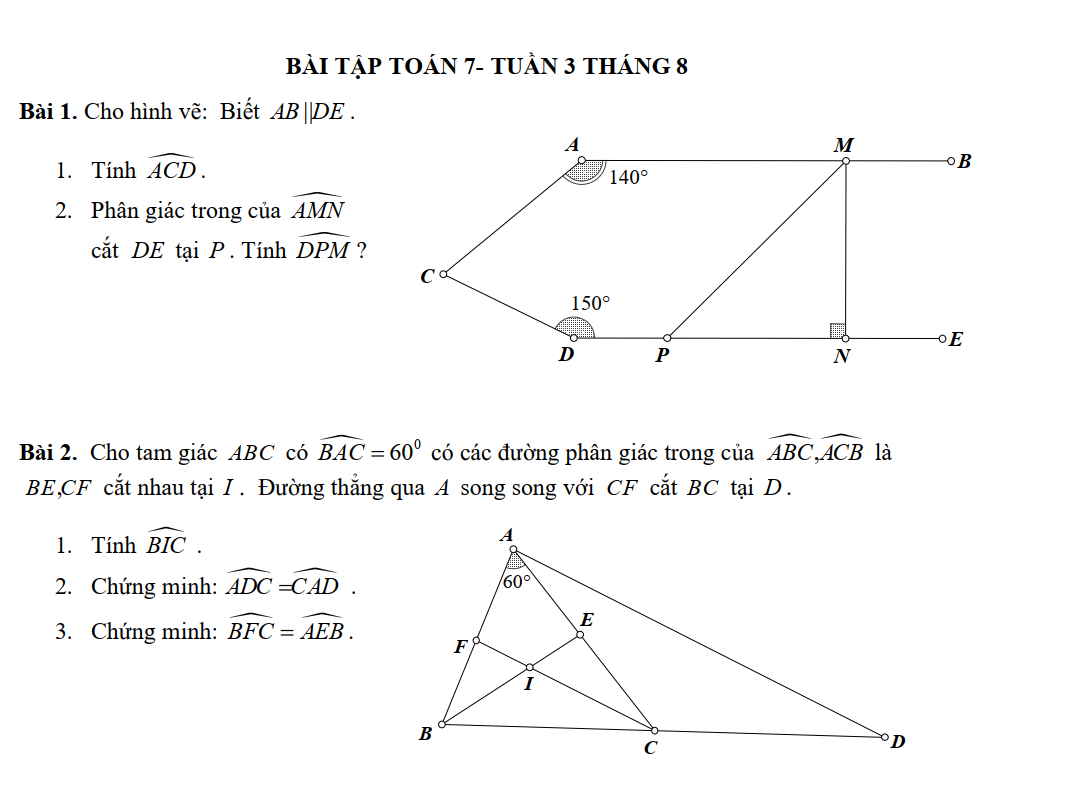
Bài 1:
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)
12 tháng 4 2020
Màn đêm buông xuống thật nhanh, trên khắp đường phố, nhà nhà đã lên đèn. Ánh điện sáng lung linh. Nhưng chỉ ít phút sau, mặt trăng tròn vành vạnh đã nhô lên. Cả gia đình tôi quây quần trên chiếc chiếu nhỏ đặt trước hiên nhà, ngồi ngắm trăng. Ôi! Thật đẹp! Cái bóng dáng tròn vành vạnh của trăng trông giống như cái đóa bạc khổng lồ treo lơ lửng trên nền trời xanh thẳm. Trăng lấp ló lờ mờ ẩn hiện sau ngọn phi lao. Gió thổi nhè nhẹ lướt qua như đang thì thầm trò chuyện. Ngoài vườn, gió luồn qua từng kẽ lá hiu hiu thổi mát, hoà lên một bản nhạc du dương, thích thú làm sao? Vui mừng, hớn hở, nôn nao. Nhớ những hôm tôi và bọn trẻ trong xóm chơi trốn tìm, tiếng cười nói nhộn nhịp khắp xóm. Làng xóm tưng bừng tiếng cười nói râm ran. Ánh trăng vằng vặc soi sáng từng cảnh vật. Ai nấy đều mong muốn cho thời gian quay trở lại để cùng nhau được hưởng sự thú vị của những đêm trăng sáng như đêm nay.
LN
20 tháng 4 2017
1)ròng rọc cố định:Giup thay đổi hướng kéo của vật
ròng rọc động:giúp giảm trọng lượng của vật so với lực kéo lên trực tiếp
2)khi bị đốt nóng,băng kép cong về phía kim loại giãn nở vì nhiệt ít hơn
khi bị làm lạnh:băng kép cong về phía kim loại giãn nở vì nhiệt nhiều hơn
3)nguyên tắc hoat động của nhiệt kế:dựa trên dự co giãn vì nhiệt của các chất
28 tháng 1 2021
Ta có: \(n_{H_2}=\dfrac{15,68}{22,4}=0,7\left(mol\right)\)
Gọi a và b lần lượt là số mol của Al và Fe
Bảo toàn mol e: \(3a+2b=1,4\)
Mà \(27a+56b=27,8\)
\(\Rightarrow\left\{{}\begin{matrix}a=0,2\\b=0,4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{0,2\cdot27}{27,8}\cdot100\approx19,42\%\\\%m_{Fe}=80,58\%\end{matrix}\right.\)
MN
28 tháng 1 2021
Đặt :
nAl = a mol
nFe = b mol
mB = 27a + 56b = 27.8 (g) (1)
2Al + 6HCl => 2AlCl3 + 3H2
a___________________1.5a
Fe + 2HCl => FeCl2 + H2
b__________________b
nH2 = 1.5a + b = 15.68/22.4 = 0.7 (mol) (2)
(1) , (2) :
a = 0.2
b = 0.4
%Al = 5.4/27.8 * 100% = 19.42%
%Fe = 100 - 19.42 = 80.58%
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
2\(\sqrt{\dfrac{16}{3}}\) - 3\(\sqrt{\dfrac{1}{27}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{3}{3\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{8}{\sqrt{3}}\) - \(\dfrac{1}{\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{16}{2\sqrt{3}}\) - \(\dfrac{2}{2\sqrt{3}}\) - \(\dfrac{3}{2\sqrt{3}}\)
= \(\dfrac{11}{2\sqrt{3}}\)
= \(\dfrac{11\sqrt{3}}{6}\)
f, 2\(\sqrt{\dfrac{1}{2}}\)- \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{2}{\sqrt{2}}\) - \(\dfrac{2}{\sqrt{2}}\) + \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5}{2\sqrt{2}}\)
= \(\dfrac{5\sqrt{2}}{4}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
13 tháng 7 2023
(1 + \(\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)).(1- \(\dfrac{3+\sqrt{3}}{\sqrt{3}+1}\))
= \(\dfrac{\sqrt{3}-1+3-\sqrt{3}}{\sqrt{3}-1}\).\(\dfrac{\sqrt{3}+1-3+\sqrt{3}}{\sqrt{3}+1}\)
= \(\dfrac{2}{\sqrt{3}-1}\).\(\dfrac{-2}{\sqrt{3}+1}\)
= \(\dfrac{-4}{3-1}\)
= \(\dfrac{-4}{2}\)
= -2
Ta có: \(a^2-1=a^2-a+a-1=\left(a+1\right)\left(a-1\right)\)
\(D=\frac{1}{2^2-1}+\frac{1}{3^2-1}+\frac{1}{4^2-1}+...+\frac{1}{20^2-1}\)
\(=\frac{1}{1.3}+\frac{1}{2.4}+\frac{1}{3.5}+...+\frac{1}{19.21}\)
\(=\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{2.4}+\frac{2}{3.5}+...+\frac{2}{19.21}\right)\)
\(=\frac{1}{2}\left(\frac{3-1}{1.3}+\frac{4-2}{2.4}+\frac{5-3}{3.5}+...+\frac{21-19}{19.21}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{2}-\frac{1}{4}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{19}-\frac{1}{21}\right)\)
\(=\frac{1}{2}\left(1+\frac{1}{2}-\frac{1}{20}-\frac{1}{21}\right)\)
\(=\frac{589}{840}\)
\(E=\frac{1}{2^3-2}+\frac{1}{3^3-3}+\frac{1}{4^3-4}+...+\frac{1}{20^3-20}\)
\(=\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{19.20.21}\)
\(=\frac{1}{2}\left(\frac{2}{1.2.3}+\frac{2}{2.3.4}+\frac{2}{3.4.5}+...+\frac{2}{19.20.21}\right)\)
\(=\frac{1}{2}\left(\frac{3-1}{1.2.3}+\frac{4-2}{2.3.4}+\frac{5-3}{3.4.5}+...+\frac{21-19}{19.20.21}\right)\)
\(=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{2.3}+\frac{1}{2.3}-\frac{1}{3.4}+\frac{1}{3.4}-\frac{1}{4.5}+...+\frac{1}{19.20}-\frac{1}{20.21}\right)\)
\(=\frac{1}{2}\left(\frac{1}{1.2}-\frac{1}{20.21}\right)\)
\(=\frac{209}{840}\)