Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1.
a. Ta có: \(AB^2+AC^2=6^2+8^2=36+64=100\)
\(BC^2=10^2=100\)
\(\Rightarrow AB^2+AC^2=BC^2\) \(\Rightarrow\Delta\)ABC vuông tại A
b. \(\Delta\)ABC vuông tại A, đường cao AH. Ta có:
AB.AC = AH.BC
hay 6.8 = AH.10
=> AH = \(\dfrac{6.8}{10}=4.8\)
bài 2:
ta có: AB<AC<BC(Vì 3cm<4cm<5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
bài 2:
ta có: AB <AC <BC (Vì 3cm <4cm <5cm)
=> góc C>góc A> góc B (Các cạnh và góc đồi diện trong tam giác)
Bài 3:
*Xét tam giác ABC, có:
góc A+góc B+góc c= 180 độ( tổng 3 góc 1 tam giác)
hay góc A+60 độ +40 độ=180độ
=> góc A= 180 độ-60 độ-40 độ.
=> góc A=80 độ
Ta có: góc A>góc B>góc C(vì 80 độ>60 độ>40 độ)
=> BC>AC>AB( Các cạnh và góc đối diện trong tam giác)
HT mik làm giống bạn Dương Mạnh Quyết
Bài 1:
a: Xét ΔABC có \(AC^2=AB^2+BC^2\)
nên ΔABC vuông tại B
b: XétΔABC có BC<AB<AC
nên \(\widehat{A}< \widehat{C}< \widehat{B}\)
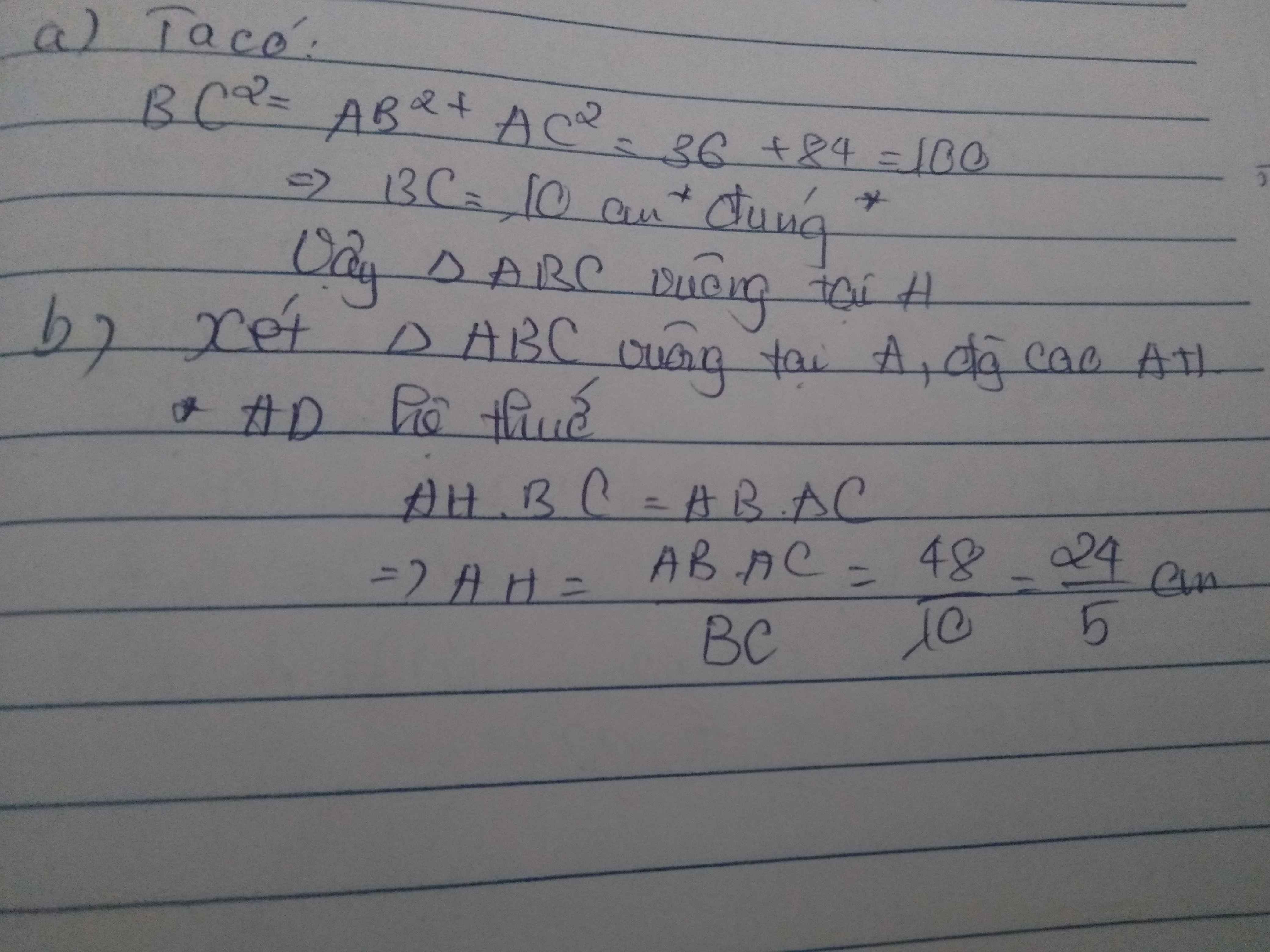
Ta có hình vẽ:
a) Xét Δ AMB và Δ EMC có:
BM = CM (gt)
AMB = EMC (đối đỉnh)
AM = ME (gt)
Do đó, Δ AMB = Δ EMC (c.g.c) (đpcm)
b) Vì Δ AMB = Δ EMC (câu a) => ABM = ECM (2 góc tương ứng)
Mà ABM và ECM là 2 góc so le trong nên AB // EC (đpcm)
c) Vì AB // EC (câu b) => CAB = FCE (đồng vị)
Δ AMB = Δ EMC (câu a) => AB = EC (2 cạnh tương ứng)
Xét Δ ABC và Δ CEF có:
AC = CF (gt)
BAC = ECF (cmt)
AB = EC (cmt)
Do đó, Δ ABC = Δ CEF (c.g.c) (1)
Dễ dàng => Δ AMC = Δ EMB (c.g.c)
=> ACM = EBM (2 góc tương ứng)
Mà ACM và EBM là 2 góc so le trong nên AC // BE
Xét Δ ABC và Δ ECB có:
ABC = BCE (vì AB // EC, ABC và BCE là 2 góc so le trong)
BC là cạnh chung
ACB = EBC (vì AC // BE; ACB và EBC là 2 góc so le trong)
Do đó, Δ ABC = Δ ECB (g.c.g) (2)
Từ (1) và (2) => Δ CEF = Δ ECB hay Δ FEC = Δ BCE (đpcm)
d) Vì Δ ABC = ECB (câu c) nên AC = BE (2 cạnh tương ứng)
Xét Δ ABC và Δ BDE có:
AB = BD (gt)
BAC = DBE (vì AC // BE, BAC và DBE là 2 góc đồng vị)
AC = BE (cmt)
Do đó, Δ ABC = Δ BDE (c.g.c)
Mà Δ ABC = Δ ECB (câu b) nên Δ BDE = Δ ECB
=> BED = EBC (2 góc tương ứng)
Mà BED và EBC là 2 góc so le trong nên BC // DE (*)
Vì Δ ECB = Δ CEF (câu c) nên BCE = FEC (2 góc tương ứng)
Mà BCE và FEC là 2 góc so le trong nên BC // EF (**)
TỪ (*) và (**) => DE trùng với EF hay 3 điểm D, E, F thẳng hàng (đpcm)
Sao bạn vẽ đc hình vậy ?