Tìm tất cả các số nguyên a để phương trình x2 - (3+2a)x + 40 - a = 0 có nghiệm nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 4 2022
\(\Delta=\left(2m+3\right)^2-4\left(40-m\right)=4m^2+16m-151\)
Phương trình có nghiệm nguyên khi \(\Delta\) là số chính phương
\(\Rightarrow4m^2+16m-151=k^2\) với \(k\in Z\)
\(\Rightarrow\left(2m+4\right)^2-167=k^2\)
\(\Rightarrow\left(2m+4-k\right)\left(2m+4+k\right)=167=1.167=167.1=-1.\left(-167\right)=-167.\left(-1\right)\)
Bảng giá trị:
| 2m+4-k | 1 | 167 | -1 | -167 |
| 2m+4+k | 167 | 1 | -167 | -1 |
| m | 40 | 40 | -44 | -44 |
Vậy \(m=\left\{-44;40\right\}\)
25 tháng 11 2023
Xét phương trình hoành độ giao điểm\(x^2\)+4x-m=0 <=> x^2+4x=m, đây là kết hợp của 2 hàm số (P):y=\(x^2\)+4x và (d):y=m.
Khi vẽ đồ thị ta thấy parabol đồng biến trên khoảng (-2;+∞)=> Điểm giao giữa parabol và đồ thị y=m là điểm duy nhất thỏa mãn phương trình có duy nhất 1 nghiệm thuộc khoảng (-3;1).Vậy để phương trình có 1 nghiệm duy nhất <=> delta=0 <=>16+4m=0<=>m=-4.
mình trình bày hơi dài mong bạn thông cảm 
CM
6 tháng 4 2018
Chọn C.
Bất phương trình
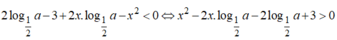
Đặt ,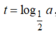 
khi đó bất phương trình trở thành x2-2tx-2t+3> 0 (*)
Bất phương trình (*) nghiệm đúng với mọi x khi và chỉ khi
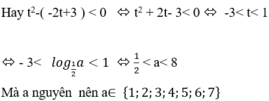
Vậy có tất cả 7 giá trị nguyên của a thỏa mãn yêu cầu bài toán.
4 tháng 7 2021
\(\Delta=m^2-4\left(m-4\right)=\left(m^2-4m+4\right)+12=\left(m-2\right)^2+12>0;\forall m\)
Suy ra pt luôn có hai nghiệm pb với mọi m
Theo viet có:\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=m-4\end{matrix}\right.\)
\(\left(5x_1-1\right)\left(5x_2-1\right)< 0\)
\(\Leftrightarrow25x_1x_2-5\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow25\left(m-4\right)-5m+1< 0\)
\(\Leftrightarrow m< \dfrac{99}{20}\)
Vậy...
AT
4 tháng 7 2021
\(\Delta=m^2-4m+16=\left(m-2\right)^2+12>0\)
\(\Rightarrow\) pt luôn có 2 nghiệm phân biệt
Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-4\end{matrix}\right.\)
Ta có: \(\left(5x_1-1\right)\left(5x_2-1\right)=25x_1x_2-5\left(x_1+x_2\right)+1\)
\(=25\left(m-4\right)-5m+1=20m-99\)
\(\Rightarrow20m-99< 0\Rightarrow m< \dfrac{99}{20}\)
DP
1 tháng 12 2021
Đk để pt trên có 2 nghiệm phân biệt x1,x2 : a>0 và denta>0
suy ra denta= (2m+1)^2-4.(m^2+1)>0
suy ra : m>3/4
Ta có P=x1x2/x1+x2=(m^2+1)/(2m+1)
Ta có: P∈Z
⇒4P∈Z
⇒(4m^2+4)/2m+1=(2m-1)+5/2m+1∈Z
⇒2m+1=Ư(5)={−5;−1;1;5}
⇒m={−3;−1;0;2}
Kết hợp đk m>3/4 ta được m=2
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 6 2021
\(\left(3^x-27\right)\left(x^2-x-20\right)\ge0\Leftrightarrow\left[{}\begin{matrix}-4\le x\le3\\x\ge5\end{matrix}\right.\)
\(\Rightarrow\) Có \(8+40-5+1=44\) nghiệm nguyên
a= {0;6;12}
a={-42;-14;-8;0;6;12}