22h tối nay là mk phải nộp rồi mong mọi người giúp cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: \(A=x^2-10x+25-34=\left(x-5\right)^2-34\ge-34\forall x\)
Dấu '=' xảu ra khi x=5
\(1,C=x^2+x-3\\ \Rightarrow C=\left(x^2+x+\dfrac{1}{4}\right)-\dfrac{13}{4}\\ \Rightarrow C=\left(x+\dfrac{1}{2}\right)^2-\dfrac{13}{4}\ge-\dfrac{13}{4}\)
dấu "=" xảy ra \(\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy \(C_{min}=-\dfrac{13}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
\(2,A=x^2-10x-9\\ \Rightarrow A=\left(x^2-10x+25\right)-34\\ \Rightarrow A=\left(x-5\right)^2-34\)
dấu "=" xảy ra \(\Leftrightarrow x=5\)
Vậy \(A_{min}=-34\Leftrightarrow x=5\)

uses crt;
var st:string;
d,i,t,x,y,a,b:integer;
begin
clrscr;
readln(st);
d:=length(st);
for i:=1 to d do write(st[i]:4);
writeln;
t:=0;
for i:=1 to d do
begin
val(st[i],x,y);
t:=t+x;
end;
writeln(t);
val(st[d],a,b);
if (a mod 2=0) then write(1)
else write(-1);
readln;
end.

#include <bits/stdc++.h>
using namespace std;
long long a[1000],i,n,t,dem,t1;
int main()
{
cin>>n;
for (i=1; i<=n; i++) cin>>a[i];
t=0;
for (i=1; i<=n; i++) if (a[i]%2==0) t+=a[i];
cout<<t<<endl;
t1=0;
dem1=0;
for (i=1; i<=n; i++)
if (a[i]<0)
{
cout<<a[i]<<" ";
t1+=a[i];
dem1++;
}
cout<<endl;
cout<<fixed<<setprecision(1)<<(t1*1.0)/(dem1*1.0);
return 0;
}

#include <bits/stdc++.h>
using namespace std;
long long a,b;
//chuongtrinhcon
long long gcd(long long a,long long b)
{
if (b==0) return(a);
return gcd(b,a%b);
}
//chuongtrinhchinh
int main()
{
cin>>a>>b;
cout<<max(a,b)<<endl;
cout<<gcd(a,b)<<endl;
if ((a>0 && b>0) or (a<0 && b<0)) cout<<a/gcd(a,b)<<" "<<b/gcd(a,b);
else cout<<"-"<<-a/gcd(-a,b)<<" "<<b/gcd(-a,b);
return 0;
}

Bài 8:
a) Ta có: \(A=\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2-2xy+y^2+3xy\right)\)
\(=\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
b) Ta có: \(B=\left(x+y\right)^3+3\left(x-y\right)\left(x+y\right)^2+3\left(x-y\right)^2\left(x+y\right)+\left(x-y\right)^3\)
\(=\left(x+y+x-y\right)^3\)
\(=\left(2x\right)^3=8x^3\)





 Mọi người cứu em, tối nay phải nộp rồi.
Mọi người cứu em, tối nay phải nộp rồi.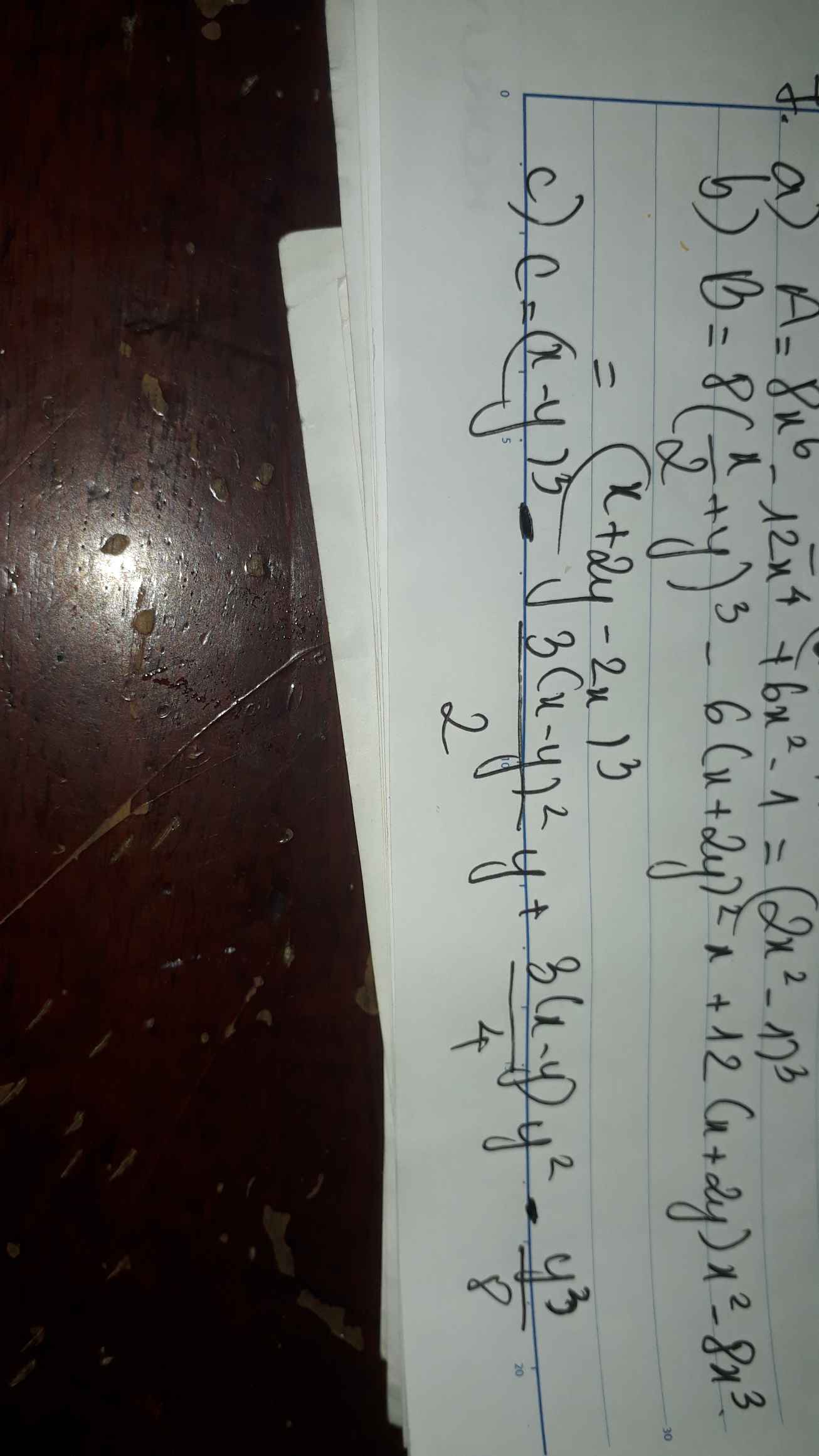

- Ta có:
\(f\left(x\right)=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)+1\)
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1\)
Đặt: \(\left(x^2+5x+5\right)=a\) ta được:
\(=\left(a-1\right)\left(a+1\right)+1\)
\(=a^2-1+1=a^2\)
Thay lại \(a=\left(x^2+5x+5\right)\) được:
\(\left(x^2+5x+5\right)^2\)
- Đối chiếu với \(\left(ax^2+bx+c\right)^2\)
Vậy \(a=1;b=5;c=5\)