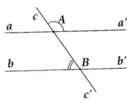
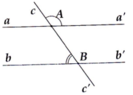
Cho hình vẽ bên. Hai đường thẳng aa’ và bb’có song song với nhau không ? Vì sao
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: c A a ' ^ + a ' A B ^ = 180° (hai góc kề bù)
=> a ' A B ^ = 180 ° − c A a ' ^ = 180 ° − 120 ° = 60 °
=> a ' A B ^ = A B b ^ = 60 ° (hai góc so le trong bằng nhau)
=> aa' // bb'

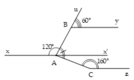
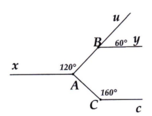
Kẻ tia Ax' là tia đối của tia Ax
Khi đó:
x ' A B ^ = u B y ^ = 60 °
⇒ A x ' // B y
Cũng có:
x ' A C ^ = 80 ° − 60 ° = 20 ° .
⇒ x ' A C ^ + A C z ^ = 180 °
⇒ A x ' // C z .
Do đó các tia A x , B y , C z nằm trên ba đường thẳng song song với nhau

Tương tự 1A
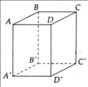
a) AB' và C'D song song, B'D' và AD chéo nhau, AC và A'C' song song.
b) BC' song song với (ADD'A').
c) AC' và CA' cắt nhau tại C.
d) (ACC'A') và (BDD'B') cắt nhau theo giao tuyến OO' (O và O' lần lượt là giao của AC, BD và A'C', B'D')

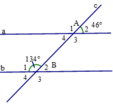
a) Ta có A ^ 2 + A ^ 3 = 180 ∘ mà A ^ 2 = 46 ∘
Do đó A ^ 3 = 180 ∘ − 46 ∘ = 134 ∘
Mặt khác B ^ 1 = 134 ∘
⇒ A ^ 3 = B ^ 1 mà hai góc này ở vị trí so le trong
=> a // b
b.
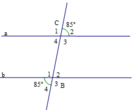
Ta có C ^ 2 = C ^ 4 = 85 ∘ (hai góc đối đỉnh)
mặt khác B ^ 4 = 85 ∘
⇒ A ^ 4 = B ^ 4 mà hai góc này ở vị trí so le trong
=> a // b
c.
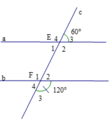
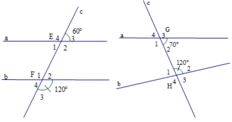
Ta có E ^ 2 + E ^ 3 = 180 ∘ (hai góc kề bù) mà E ^ 3 = 60 ∘
Do đó E ^ 2 = 180 ∘ − 60 ∘ = 120 ∘
Mặt khác F ^ 3 = 120 ∘
⇒ F ^ 3 = E ^ 2 mà hai góc này ở vị trí đồng vị
=> a // b
d.
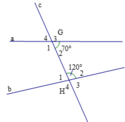
Ta có G ^ 1 + G ^ 2 = 180 ∘ (hai góc kề bù) mà G ^ 2 = 70 ∘
Do đó G ^ 1 = 180 ∘ − 70 ∘ = 110 ∘
Mà H ^ 2 = 120 ∘
⇒ G ^ 1 < H ^ 2 110 ∘ < 120 ∘ mà hai góc này ở vị trí so le trong
=> hai đường thẳng a và b không song song với nhau

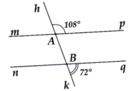
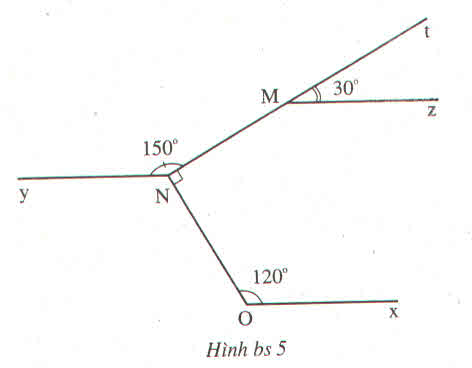
a) Vì góc tMz và góc NMz kề bù nên:
\(\widehat{tMz}+\widehat{NMz}=180^o\)
\(\Rightarrow30^o+\widehat{NMz}=180^o\)
\(\Rightarrow\widehat{NMz}=180^o-30^o=150^o\)
Ta có: \(\widehat{NMz}=\widehat{MNy}=150^o\)
\(\Rightarrow\) Mz // Ny (vì có cặp góc so le trong bằng nhau)
a) 2 đường thẳng Mz và Ny song song
b) 2 đường thẳng Ny và Ox không song song vì 2 góc so le trong không bằng nhau
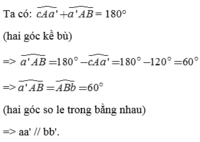


a'a không song song với b'b
Vì ở vị trí đồng vị cMa ko bằng MNb