Cho tam giác abc vuông tại a, d là trung điểm bc, d là điểm đối xứng với m qua ab ,e là giao điểm của ab và dm, n là điểm đối xứng với d qua ac, f là giao điểm của ac với dn
A.tứ giác aedf là hình gì? Vì sao
B. Tứ giác abdn là hình gì? Vì sao
C. Chứng minh ba điểm m,a,n thẳng hàng
D. Tìm điều kiện của tam giác abc để tứ giác aedf là hình vuông
(Vẽ hình đầy đủ, rõ ràng)

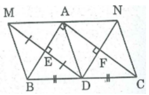
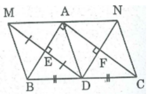


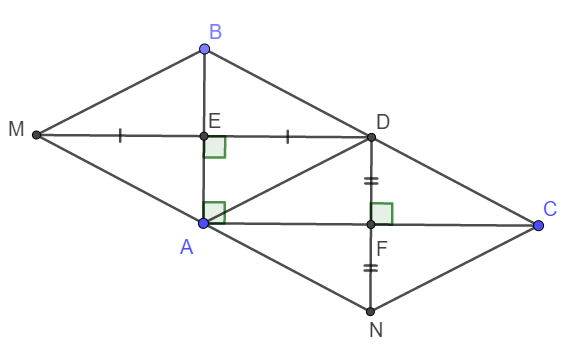
a.
DEA = EAF = AFD = 900
=> AEDF là hình chữ nhật.
b.
AB // ED (AEDF là hình chữ nhât)
D là trung điểm của BC (gt)
=> F là trung điểm của AC
=> DF là đường trung bình của tam giác CAB
=> DF = AB/2
mà DF = DN/2 (F là trung điểm của DN)
=> AB = DN
mà AB // DN
=> ABDN là hình bình hành.
c.
AC // ED (AEDF là hình chữ nhật)
D là trung điểm của BC (gt)
=> E là trung điểm của AB
mà E là trung điểm của MD
=> AMBD là hình bình hành
mà AB _I_ MD
=> AMBD là hình thoi
=> AM // BD
mà AN // BD (ABDN là hình bình hành)
=> AM \(\equiv\) AN
=> A, M, N thẳng hàng.
d.
AEDF là hình vuông
<=> AD là tia phân giác của BAC
mà AD là đường trung tuyến của tam giác ABC (D là trung điểm của BC)
=> Tam giác ABC cân tại A
mà tam giác ABC vuông tại A (gt)
=> Tam giác ABC vuông cân tại A
Vậy AEDF là hình vuông khi tam giác ABC vuông cân tại A.
AN = BD (ABDN là hình bình hành)
mà BD = DC (D là trung điểm của BC)
=> AN = DC
mà AN // DC (ABDN là hình bình hành)
=> ANCD là hình bình hành
mà AC _I_ ND
=> ANCD là hình thoi