max A=|x|.\(\sqrt{1-x^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1, A= y^3(1-y)^2 = 4/9 . y^3 . 9/4 (1-y)^2
= 4/9 .y.y.y . (3/2-3/2.y)^2
=4/9 .y.y.y (3/2-3/2.y)(3/2-3/2.y)
<= 4/9 (y+y+y+3/2-3/2.y+3/2-3/2.y)^5
=4/9 . 243/3125
=108/3125
Đến đó tự giải

$A=2x-\sqrt{x}=2(x-\frac{1}{2}\sqrt{x}+\frac{1}{4^2})-\frac{1}{8}$
$=2(\sqrt{x}-\frac{1}{4})^2-\frac{1}{8}$
$\geq \frac{-1}{8}$
Vậy $A_{\min}=-\frac{1}{8}$. Giá trị này đạt tại $x=\frac{1}{16}$
$B=x+\sqrt{x}$
Vì $x\geq 0$ nên $B\geq 0+\sqrt{0}=0$
Vậy $B_{\min}=0$. Giá trị này đạt tại $x=0$

\(1,yz\sqrt{x-1}=yz\sqrt{\left(x-1\right)\cdot1}\le yz\cdot\dfrac{x-1+1}{2}=\dfrac{xyz}{2}\)
\(zx\sqrt{y-2}=\dfrac{zx\cdot2\sqrt{2\left(y-2\right)}}{2\sqrt{2}}\le\dfrac{xyz}{2\sqrt{2}}\\ xy\sqrt{z-3}=\dfrac{xy\cdot2\sqrt{3\left(z-3\right)}}{2\sqrt{3}}\le\dfrac{xyz}{2\sqrt{3}}\)
\(\Leftrightarrow M\le\dfrac{\dfrac{xyz}{2}+\dfrac{xyz}{2\sqrt{2}}+\dfrac{xyz}{2\sqrt{3}}}{xyz}=\dfrac{xyz\left(\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}\right)}{xyz}=\dfrac{1}{2}+\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-1=1\\y-2=2\\z-3=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=4\\z=6\end{matrix}\right.\)
\(2,N^2=\left(\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\right)^2\\ \Leftrightarrow N^2\le\left(a+b+b+c+c+a\right)\left(1^2+1^2+1^2\right)\\ \Leftrightarrow N^2\le6\left(a+b+c\right)=6\sqrt{2}\\ \Leftrightarrow N\le\sqrt{6\sqrt{2}}\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{\sqrt{2}}{3}\)

1) ĐK: x \(\ge\)1; y \(\ge\)2
Áp dụng bđt \(\frac{\sqrt{a}+\sqrt{b}}{2}\le\)\(\sqrt{\frac{a+b}{2}}\) (cho 2 sô a;b > 0) ta co:
\(\frac{A}{2}\le\sqrt{\frac{x-1+y-2}{2}}=\sqrt{\frac{4-3}{2}}=\sqrt{\frac{1}{2}}\)
\(A=\sqrt{\frac{1}{2}}.2=\sqrt{2}\)
Dấu "=" xảy ra khi \(\left\{\begin{matrix}x-1=y-2\\x+y\end{matrix}\right.\)\(\Leftrightarrow\left\{\begin{matrix}x=\frac{3}{2}\\y=\frac{5}{2}\end{matrix}\right.\)
2) ĐK: x \(\ge\)1; y \(\ge\)2
Áp dụng bđt AM-GM cho 2 số dương ta có:
\(\frac{\sqrt{x-1}}{x}=\frac{\sqrt{1.\left(x-1\right)}}{x}\le\frac{1+x-1}{2x}=\frac{1}{2}\)
\(\frac{\sqrt{y-2}}{y}=\frac{\sqrt{2.\left(y-2\right)}}{\sqrt{2}.y}\le\frac{2+y-2}{\sqrt{2}.2y}=\frac{1}{\sqrt{2}.2}\)
\(B=\frac{\sqrt{x-1}}{x}+\frac{\sqrt{y-2}}{y}\)\(\le\frac{1}{2}+\frac{1}{\sqrt{2}.2}=\frac{2}{4}+\frac{\sqrt{2}}{4}=\frac{2+\sqrt{2}}{4}\)
Dấu "=" xảy ra khi \(\left\{\begin{matrix}x-1=1\\y-2=2\end{matrix}\right.\)\(\Leftrightarrow\left\{\begin{matrix}x=2\\y=4\end{matrix}\right.\)

DKXD của A, ta có \(x^{2\le5\Rightarrow-\sqrt{5}\le x\le\sqrt{5}}\)
mà \(3x\ge-3\sqrt{5}\)
mặt kkhác \(\sqrt{5-x^2}\ge0\Rightarrow A=3x+x\sqrt{5-x^2}\ge-3\sqrt{5}\)
min A= \(-3\sqrt{5}\)\(\Leftrightarrow x=-\sqrt{5}\)

Lời giải:
a.
Áp dụng BĐT Bunhiacopxky:
$A^2=(\sqrt{x-1}+\sqrt{9-x})^2\leq (x-1+9-x)(1+1)=16$
$\Rightarrow A\leq 4$
Vậy $A_{\max}=4$. Giá trị này đạt tại $x=5$
b.
$A=\frac{3(\sqrt{x}+2)+5}{\sqrt{x}+2}=3+\frac{5}{\sqrt{x}+2}$
Để $A$ nguyên thì $\frac{5}{\sqrt{x}+2}=m$ với $m$ nguyên dương
$\Leftrightarrow \sqrt{x}+2=\frac{5}{m}$
$\sqrt{x}=\frac{5-2m}{m}$
Vì $\sqrt{x}\geq 0$ nên $\frac{5-2m}{m}\geq 0$
Mà $m$ nguyên dương nên $5-2m\geq 0$
$\Leftrightarrow m\leq 2,5$.
$\Rightarrow m=1; 2$
$\Rightarrow x=9; x=\frac{1}{4}$

ĐKXĐ: \(x\ge0\)
Do \(\left\{{}\begin{matrix}2>0\\x+\sqrt{x}+1>0\end{matrix}\right.\) nên \(A_{max}\) khi \(x+\sqrt{x}+1\) đạt GTNN
Mà \(x\ge0\Rightarrow x+\sqrt{x}+1\ge1\)
\(\Rightarrow\dfrac{2}{x+\sqrt{x}+1}\le2\)
Hay \(A_{max}=2\) khi \(x=0\)

a: ĐKXĐ: x>=0; x<>1
\(P=\left(\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}\right)\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(x-1\right)^2}{2}\)
\(=\dfrac{x-\sqrt{x}-2-x-\sqrt{x}+2}{2}\cdot\dfrac{x-1}{\sqrt{x}+1}\)
\(=-\sqrt{x}\left(\sqrt{x}-1\right)\)
b: 0<x<1
=>căn x<1
=>căn x-1<0
=>căn x*(căn x-1)<0
=>-căn x*(căn x-1)>0
=>P>0
c: \(P=-x+\sqrt{x}-\dfrac{1}{4}+\dfrac{1}{4}\)
\(=-\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\)
Dấu = xảy ra khi x=1/4

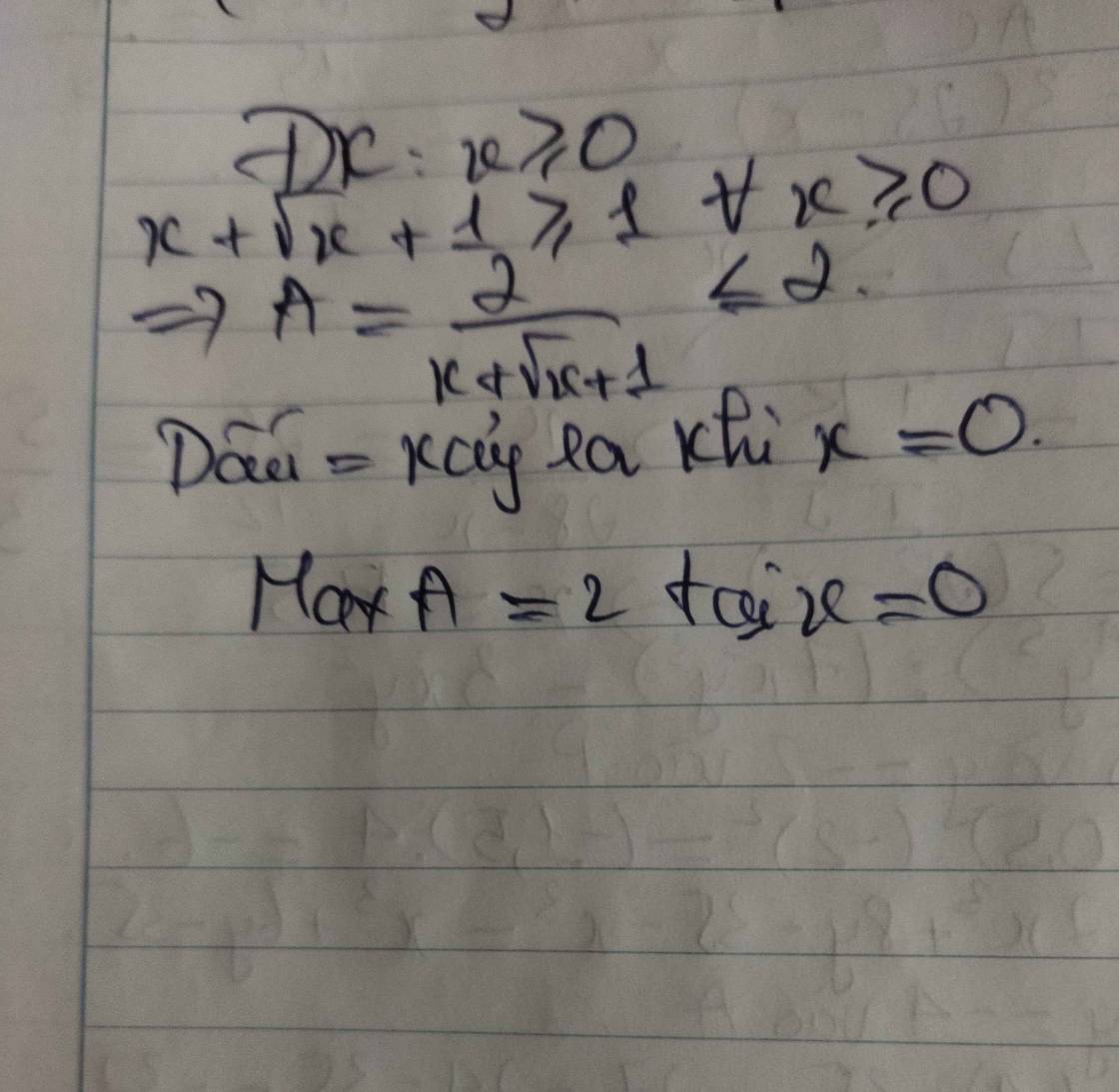
\(A=\left|x\right|\sqrt{1-x^2}\)
\(=\sqrt{x^2}\cdot\sqrt{1-x^2}\)
\(=\sqrt{x^2\left(1-x^2\right)}\)
\(\le\frac{x^2+1-x^2}{2}=\frac{1}{2}\) (Bđt Cô-si)
Dấu = khi \(x=\pm\frac{1}{\sqrt{2}}\)
Vậy \(Max_A=\frac{1}{2}\Leftrightarrow x=\pm\frac{1}{\sqrt{2}}\)
cảm ơn bạn nha nha nha nha nha nha. ahihi vui quá. tớ làm thử qua các này mà tưởng không đưa vào căn được nên vất đi luôn òi. thankssssssssssssssssss