Cho lăng trụ ABC,A'B'C' có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A' lên đáy là trung điểm I của BC. Góc giưã BC' và đáy bằng 45°. Tính V lăng trụ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
29 tháng 1 2017
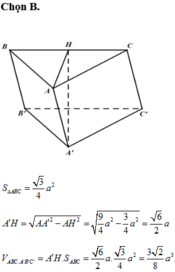
Chọn B
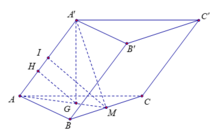
Ta có A ' G ⊥ A B C nên A ' G ⊥ B C ; B C ⊥ A M ⇒ B C ⊥ M A A '
Kẻ M I ⊥ A A ' ; B C ⊥ I M nên d A A ' ; B C = I M = a 3 4
Kẻ G H ⊥ A A ' , ta có
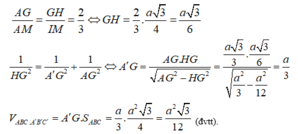

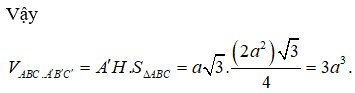
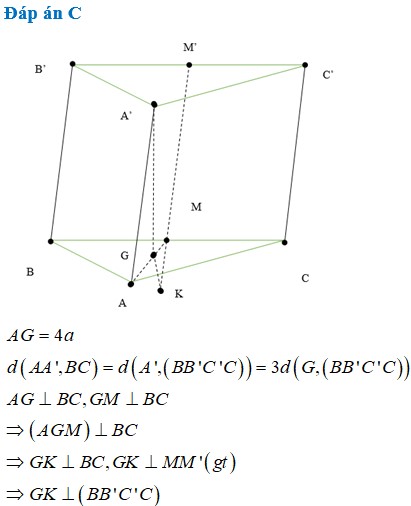
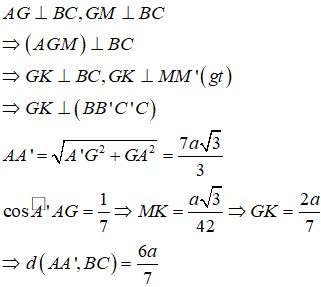
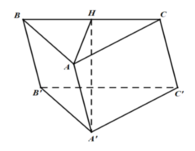
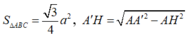
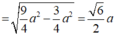
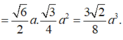
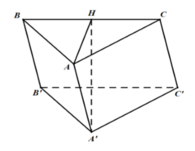
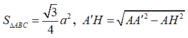
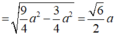
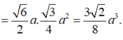
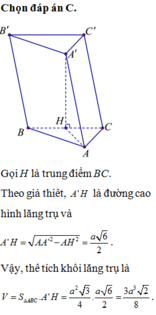
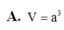
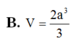
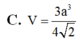
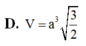
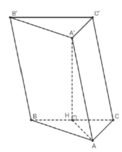

+) Đầu tiên phải dựng hình chiếu vuông góc của C' trên (ABC)
Lấy điểm M trên mp(ABC) sao cho AIMC là hình bình hành
dễ dàng chứng minh M là hình chiếu vuông góc của C' trên (ABC)
+) Góc giữa BC' và (ABC) chính là \(\widehat{MBC'}\)=45o
MC' là chều cao của lăng trụ đối với đáy ABC
+) Tính được BM= \(\sqrt{MC^2+BC^2}=a\sqrt{2}\)
MC'=BM.tan\(\widehat{MBC'}\)=\(a\sqrt{2}.tan45^o\) =\(a\sqrt{2}\)
V lăng trụ= MC'.SABC=\(a\sqrt{2}.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{6}}{4}\)