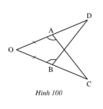
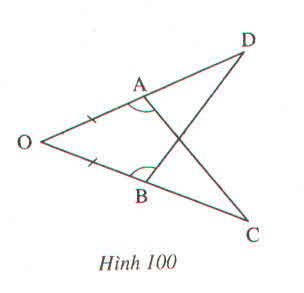
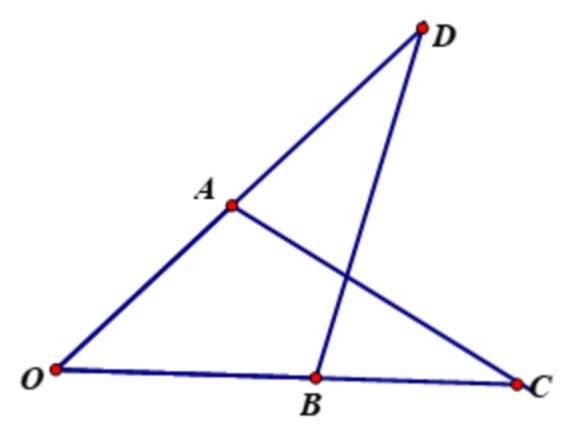
Trên hình 90, ta có OA=OB, OAC=OBD.Chứng minh AC=BD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔOAC và ΔOBD có:
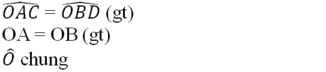
Nên ΔOAC = ΔOBD (g.c.g)
Suy ra AC = BD (hai cạnh tương ứng).

a: Xét ΔOBD và ΔOAC có
\(\widehat{OBD}=\widehat{OAC}\)
OB=OA
\(\widehat{BOD}\) chung
Do đó: ΔOBD=ΔOAC
=>BD=AC; OD=OC
OB+BC=OC
OA+AD=OD
mà OB=OA và OC=OD
nên BC=AD
b: Xét ΔADC và ΔBCD có
AD=BC
CD chung
AC=BD
Do đó: ΔADC=ΔBCD
c: ΔADC=ΔBCD
=>\(\widehat{IDC}=\widehat{ICD}\)
=>ΔIDC cân tại I
=>ID=IC
ID+IB=BD
IC+IA=AC
mà ID=IC và BD=AC
nên IB=IA
d: Xét ΔOAI và ΔOBI có
OA=OB
AI=BI
OI chung
Do đó: ΔOAI=ΔOBI
=>\(\widehat{AOI}=\widehat{BOI}\)
=>OI là phân giác của góc AOB
=>OI là phân giác của góc COD
ΔCOD cân tại O
mà OI là đường phân giác
nên OI\(\perp\)CD

a. Xét \(2\Delta\): \(\Delta AOC\) và \(\Delta BOC\) có:
\(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\AC=BC\left(gt\right)\\OC.chung\end{matrix}\right.\)
\(\Rightarrow\Delta AOC=\Delta BOC\left(c.c.c\right)\)
b. Theo câu a, suy ra:
\(\widehat{OAC}=\widehat{OBC}\)
Mà: \(\widehat{OAC}=110^o\)
\(\Rightarrow\widehat{OBC}=110^o\)
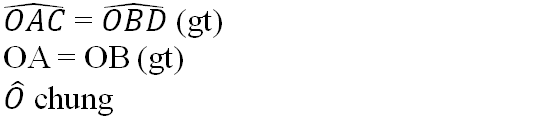

Sao thấy bạn nói "trên hình 90" mà hổng thấy hình đâu?
???????