tính nguyên hàm \(\int xcosxdx\) ọi người giúp với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 5 2018
Chọn B
Đặt u = 1 - x d v = cos x d x ⇒ d u = - d x v = sin x
⇒ ∫ 1 - x cos x d x = 1 - x sin x + ∫ sin x d x = 1 - x sin x - cos x + C
AM
10 tháng 2 2022
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
17 tháng 3 2020
em ơi em chưa nói x thuộc gì nữa bọn anh học tới x thuộc R lậy còn nêu như x thuộc Z thì: \(x\in\left\{x=ℤ\backslash-20< x< 21\right\}\)
SC
12 tháng 1 2022
Tuyệt vời, đợi mình load rồi mình hỏi thêm vào câu nữa nha bẹn
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
1.
\(I=\int\dfrac{cot^2x}{sin^6x}dx=\int\dfrac{cot^2x}{sin^4x}.\dfrac{1}{sin^2x}=\int cot^2x\left(1+cot^2x\right)^2.\dfrac{1}{sin^2x}dx\)
Đặt \(u=cotx\Rightarrow du=-\dfrac{1}{sin^2x}dx\)
\(I=-\int u^2\left(1+u^2\right)^2du=-\int\left(u^6+2u^4+u^2\right)du\)
\(=-\dfrac{1}{7}u^7+\dfrac{2}{5}u^5+\dfrac{1}{3}u^3+C\)
\(=-\dfrac{1}{7}cot^7x+\dfrac{2}{5}cot^5x+\dfrac{1}{3}cot^3x+C\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
2.
\(I=\int\left(e^{sinx}+cosx\right).cosxdx=\int e^{sinx}.cosxdx+\int cos^2xdx\)
\(=\int e^{sinx}.d\left(sinx\right)+\dfrac{1}{2}\int\left(1+cos2x\right)dx\)
\(=e^{sinx}+\dfrac{1}{2}x+\dfrac{1}{4}sin2x+C\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2022
\(\int sin^2\dfrac{x}{2}dx=\int\left(\dfrac{1}{2}-\dfrac{1}{2}cosx\right)dx=\dfrac{1}{2}x-\dfrac{1}{2}sinx+C\)
\(\int cos^23xdx=\int\left(\dfrac{1}{2}+\dfrac{1}{2}cos6x\right)dx=\dfrac{1}{2}x+\dfrac{1}{12}sin6x+C\)
\(\int4cos^2\dfrac{x}{2}dx=\int\left(2+2cosx\right)dx=2x+2sinx+C\)
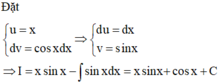
\(\int xcosx.dx=\int\left(xcosx+sinx\right)dx+\int\left(-sinx\right)dx\) = \(xsinx+cosx+C\)
cảm ơn bạn/ bạn có fb k cho mình xin ạ