tính nguyên hàm của e\(^{x^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 6 2018
Đáp án B
Ta có ∫ 0 1 e − 2 x + 3 d x = F 1 − F 0 ⇔ e − 2 x + 3 − 2 | 0 1 = e − F 0 ⇔ − e 2 + e 3 2 = e − F 0
Do đó F 0 = 3 e − e 3 2
HT
15 tháng 3 2021
\(\int e^x\left(2-x\right)dx\)
\(\left\{{}\begin{matrix}u=2-x\\dv=e^xdx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=-dx\\v=e^x\end{matrix}\right.\)
\(\Rightarrow\int e^x\left(2-x\right)dx=e^x\left(2-x\right)+\int e^xdx=e^x\left(2-x\right)+e^x\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
2.
\(I=\int e^{3x}.3^xdx\)
Đặt \(\left\{{}\begin{matrix}u=3^x\\dv=e^{3x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=3^xln3dx\\v=\dfrac{1}{3}e^{3x}\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}\int e^{3x}.3^xdx=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}.I\)
\(\Rightarrow\left(1+\dfrac{ln3}{3}\right)I=\dfrac{1}{3}e^{3x}.3^x\)
\(\Rightarrow I=\dfrac{1}{3+ln3}.e^{3x}.3^x+C\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 3 2022
1.
\(I=\int\left(2x-1\right)e^{\dfrac{1}{x}}dx=\int2x.e^{\dfrac{1}{x}}dx-\int e^{\dfrac{1}{x}}dx\)
Xét \(J=\int2x.e^{\dfrac{1}{x}}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{\dfrac{1}{x}}\\dv=2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\dfrac{e^{\dfrac{1}{x}}}{x^2}dx\\v=x^2\end{matrix}\right.\)
\(\Rightarrow J=x^2.e^{\dfrac{1}{x}}+\int e^{\dfrac{1}{x}}dx\)
\(\Rightarrow I=x^2.e^{\dfrac{1}{x}}+C\)
18 tháng 12 2016
\(\int\frac{2^{x-1}}{e^x}dx=\frac{1}{2}\int\left(\frac{2}{e}\right)^xdx=\frac{1}{2}.\frac{\left(\frac{2}{e}\right)^x}{ln\left(\frac{2}{e}\right)}+C=\frac{2^x}{2e^x\left(ln2-1\right)}+C\)
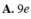
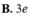
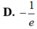
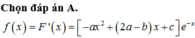
đặt x2=t \(\Rightarrow\) x=\(\pm\) \(\sqrt{t}\) và \(dx=\pm d\sqrt{t}\)
ta có A=\(\int e^{x^2}dx=\pm\int e^td\left(\sqrt{t}\right)\)
theo phương pháp nguyên hàm từng phần ta có
A=\(\pm\left[e^t\sqrt{t}-e^t\int\sqrt{t}\right]\)
=\(\pm\left[e^t\sqrt{t}-\frac{3}{2}.e^t.\sqrt[3]{t^2}\right]\)+C
Thay t=x2 vào ta tìm được 2 họ nguyên hàm của \(e^{x^2}\)
cảm ơn cậu nhiều