Bài 1: Cmr các số sau đây là số chinh phương
a) B= x.(x-y) . ( x+y) . ( x+2y) + y4
b) C= ( x-y). ( x-2y) . ( x-3y) . ( x-4y) + y4
Làm nhanh giúp mình nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
6 tháng 2 2022
Đúng(0)
Những câu hỏi liên quan
6 tháng 2 2022
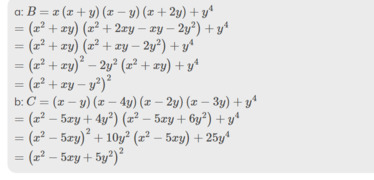
a: \(B=x\left(x+y\right)\left(x-y\right)\left(x+2y\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+2xy-xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)\left(x^2+xy-2y^2\right)+y^4\)
\(=\left(x^2+xy\right)^2-2y^2\left(x^2+xy\right)+y^4\)
\(=\left(x^2+xy-y^2\right)^2\)
b: \(C=\left(x-y\right)\left(x-4y\right)\left(x-2y\right)\left(x-3y\right)+y^4\)
\(=\left(x^2-5xy+4y^2\right)\left(x^2-5xy+6y^2\right)+y^4\)
\(=\left(x^2-5xy\right)^2+10y^2\left(x^2-5xy\right)+25y^4\)
\(=\left(x^2-5xy+5y^2\right)^2\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
a, (3 - \(x\))(4y + 1) = 20
Ư(20) = { -20; -10; -5; -4; -2; -1; 1; 2; 4; 5; 10; 20}
Lập bảng ta có:
| \(3-x\) | -20 | -10 | -5 | -4 | -2 | -1 | 1 | 2 | 4 | 5 | 10 | 20 |
| \(x\) | 23 | 13 | 8 | 7 | 5 | 4 | 2 | 1 | -1 | -2 | -7 | -17 |
| 4\(y\) + 1 | -1 | -2 | -4 | -5 | -10 | -20 | 20 | 10 | 5 | 4 | 2 | 1 |
| \(y\) | -1/2 | -3/4 | -5/4 | -6/4 | -11/4 | -21/4 | 19/4 | 9/4 | 1 | 3/4 | 1/4 | 0 |
Vậy các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) =(-1; 1); (-17; 0)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
25 tháng 6 2023
b, \(x\left(y+2\right)\)+ 2\(y\) = 6
\(x\) = \(\dfrac{6-2y}{y+2}\)
\(x\in\) Z ⇔ 6 - \(2y⋮\) \(y\) + 2 ⇒-(2y + 4) +10 ⋮ \(y\) + 2 ⇒ -2(\(y\)+2) +10 ⋮ \(y\)+2
⇒ 10 ⋮ \(y\) + 2
Ư(10) = { -10; -5; -2; -1; 1; 2; 5; 10}
Lập bảng ta có:
| \(y+2\) | -10 | -5 | -2 | -1 | 1 | 2 | 5 | 10 |
| \(y\) | -12 | -7 | -4 | -3 | -1 | 0 | 3 | 8 |
| \(x=\) \(\dfrac{6-2y}{y+2}\) | -3 | -4 | -7 | -12 | 8 | 3 | 0 | -1 |
Theo bảng trên ta có các cặp \(x;y\)
nguyên thỏa mãn đề bài lần lượt là:
(\(x;y\) ) =(-3; -12); (-4; -7); (-12; -3); (8; -1); (3; 0); (0;3 (-1; 8)
V
0
TN
15 tháng 7 2016
Bài 1:
A=x2 +y2 -2x-2y+2xy+5
=x2 +y2 -2x-2y+2xy+1+4
=xy+x2-x+xy+y2-y-y-x+1+4
=x(x+y-1)+y(x+y-1)-1(x+y-1)
=(x+y-1)(x+y-1)
=(x+y-1)2+4.Với x+y=3
=>A=(3-1)2+4=22+4=8
Bài 2:
B=x^2 +4y^2-2x-4y-4xy+10
=-2xy+x2-x-2xy+4y2+2y-x+2y+1-8y+9
=x(x-2y-1)-2y(x-2y-1)-1(x-2y-1)-8y+9
=(x-2y-1)(x-2y-1)-8y+9
=(x-2y-1)2-8y+9
Với x-2y=5.Ta có:... tự thay
Bài 3: chịu
4 tháng 4 2019
a)Để phân số x-3/x+17 là số nguyên thì:
=>x-3 chia hết cho x+17
=>x+17-20 chia hết cho x+17
=>(x+17)-20 chia hết cho x+17
<=>20 chia hết cho x+17
<=>x+17 là ước của 20
Ta có: Ư(20)={1;-1;2,-2;4;-4;5;-5;10;-10;20;-20}
...
Bạn tự làm tiếp nha!
^=^
4 tháng 4 2019
b)để phân số 3x-1/x-6 thì:
3x-1 chia hết cho x-6
=>(3x-18)+17 chia hết cho x-6
=>3(x-6)+17 chia hết cho x-6
<=>17 chia hết cho x-16
...
tương tự như câu a) nha
P
2
16 tháng 8 2016
Ta có \(A=\left(x+y\right)\left(x+2y\right)\left(x+3y\right)\left(x+4y\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+6y^2\right)+y^4\)
Đặt \(x^2+5xy+5y^2=t\) thì:
\(A=\left(t-y^2\right)\left(t+y^2\right)+y^4=t^2-y^4+y^4=t^2=\left(x^2+5xy+5y^2\right)^2\)
Vì \(x,y\in Z\) nên \(x^2\in Z,\)\(5xy\in Z,\)\(5y^2\in Z\)\(\Rightarrow\)\(x^2+5xy+5y^2\in Z\)
Vậy A là số chính phương.