Trong tam giác ABC đường cao AH tạo với các cạnh AB, AC 2 góc sao cho BAH=2.CAH.Biết góc A =72 độ .Tính góc B và C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(cậu tự vẽ hình nhé)
Vì góc BAH= 2 lần góc CAH mà góc BAC+ góc CAH = góc BAH -> góc CAH= góc BAC = 72 độ;
Ta có: AH// BC -> góc CAH= góc BCA = 72 độ ( 2 góc so le trong);
Tam giác ABC có: góc BAC + góc BCA + góc ABC = 180độ (t/c tổng 3 góc trong 1 tam giác);
mà góc BAC và góc BCA = 72độ(cmt) -> góc ABC = 180 độ - 72 độ - 72 độ=36 độ
Vậy góc B= 36 độ, góc C= 72 độ.

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

Tam giác ABC vuông tại A \(\Rightarrow\) góc B + góc C = 90 độ (1)
\(\Rightarrow\) góc C = 90 độ - góc B = 90 độ - 72 độ = 18 độ
Tam giác ABH vuông tại H \(\Rightarrow\) góc B + góc A1 = 90 độ (2)
(1),(2) \(\Rightarrow\) góc C = góc A1 \(\Rightarrow\) góc A1 = 18 độ

3:
\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
HB=12^2/20=7,2cm
=>HC=20-7,2=12,8cm
\(AD=\dfrac{2\cdot12\cdot16}{12+16}\cdot cos45=\dfrac{48\sqrt{2}}{7}\)
\(HD=\sqrt{AD^2-AH^2}=\dfrac{48}{35}\left(cm\right)\)

`a)`
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
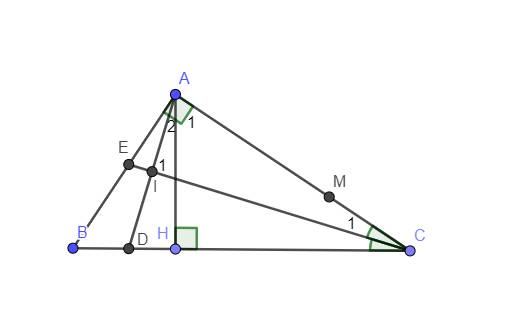
Ta có hình vẽ:
Xét Δ ABC có: ACB + CAB + ABC = 180o (tổng 3 góc của Δ)
=> ACB + ABC + 72o = 180o
=> ACB + ABC = 180o - 72o = 108o
Vì AH là đường cao của Δ ABC nên \(AH\perp BC\)
Δ vuông ACH có: ACH + CAH = 90o (1)
Δ vuông ABH có: ABH + BAH = 90o (2)
Từ (1) và (2) => ACH + CAH + ABH + BAH = 90o + 90o
=> 108o + CAH + 2.CAH = 180o
=> 3.CAH = 180o - 108o = 72o
=> CAH = 72o : 3 = 24o
=> ACH = 90o - 24o = 66o; ABH = 108o - 66o = 42o
Vậy góc B = 42o; góc C = 66o