Cho log3=a, log5=b. Tính \(\log_{15}\)30 theo a và b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có 1350 = 30.32 . 5 suy ra
log301350 = log30(30. 32. 5) = 1 + 2log303 + log305 = 1 + 2a + b.
b) log2515 = =
=
=
=
.

\(log_{a^4}b^4.log_ba^5=\dfrac{1}{4}.4.log_ab.5.log_ba=5.log_ab.log_ba=5\)
\(log_{a^3}b^2.log_ba^4=\dfrac{1}{3}.2.log_ab.4.log_ba=\dfrac{8}{3}.log_ab.log_ba=\dfrac{8}{3}\)
\(log_{a^{15}}b^7.log_{b^{49}}a^{30}=\dfrac{1}{15}.7.log_ab.\dfrac{1}{49}.30.log_ba=\dfrac{2}{7}log_ab.log_ba=\dfrac{2}{7}\)
\(log_{a^{2021}}b^{2020}.log_{b^{4040}}a^{6063}=\dfrac{1}{2021}.2020.log_ab.\dfrac{1}{4040}.6063.log_ba=\dfrac{3}{2}\)

Bài này e rằng quá khó để tự luận do vấn đề cơ số
Nhưng tinh ý 1 chút thì giải trắc nghiệm đơn giản:
\(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}=\dfrac{x-1}{2\sqrt{x}}\)
Để ý rằng \(x-1-2\sqrt{x}=x-\left(2\sqrt{x}+1\right)\)
Do đó pt luôn có nghiệm thỏa mãn: \(x-2\sqrt{x}-1=0\Rightarrow x=3+2\sqrt{2}\)

a) \(\left(\dfrac{1}{9}\right)^{\dfrac{1}{2}log^4_3}=\left(3^{-2}\right)^{\dfrac{1}{2}log^4_3}=\left(3^{log^4_3}\right)^{-2.\dfrac{1}{2}}=4^{-1}=\dfrac{1}{4}\);
b) \(10^{3-log5}=\dfrac{10^3}{10^{log5}}=\dfrac{10^3}{5}=200\);
c) \(2log^{log1000}_{27}=2log^3_{3^3}=\dfrac{2}{3}log^3_3=\dfrac{2}{3}\);
d) \(3log_2^{log_4^{16}}+log^2_{\dfrac{1}{2}}=3log^2_2-log^2_2=3-1=2\).

Ta có :
\(a=\log_{14}7=\frac{1}{\log_7\left(2.7\right)}=\frac{1}{1+\log_72}\Rightarrow\log_72=\frac{1}{a}-1=\frac{1-1}{a}\)
\(b=\log_{15}5=\frac{\log_75}{\log_7\left(7.2\right)}=\frac{\log_72}{1+\log_72}\Rightarrow\log_75=b\left(1+\log_72\right)=b\left(1+\frac{1-a}{a}\right)=\frac{b}{a}\)
\(\Rightarrow E=\log_{35}28=\frac{\log_727}{\log_735}=\frac{\log_7\left(7.2^2\right)}{\log_7\left(7.5\right)}=\frac{1+\log_72}{1+\log_75}=\frac{1+2.\frac{1-a}{a}}{1+\frac{b}{a}}=\frac{2-a}{a+b}\)
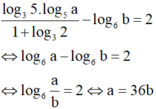
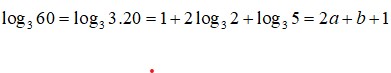
[log(10a-10b) + 1] / (a+b)
Bạn nào muốn luyện thêm Logarit thì có thể vào website http://tailieutracnghiem.net ấy