Cho ∆𝐴𝐵𝐶 𝑣𝑢ô𝑛𝑔 𝑡ạ𝑖 𝐴 ( AB < AC ) có đường cao AH. Qua C vẽ đường thẳng song song với AB cắt tia AH tại D. Cho AB = 15cm, AC = 20cm. a) Chứng minh ∆𝐴𝐻𝐵 𝑣à ∆𝐴𝐵𝐶 đồ𝑛𝑔 𝑑ạ𝑛𝑔,𝑡í𝑛ℎ 𝐵𝐶, 𝐻𝐵 , 𝐴Hb) Chứng minh 𝐴𝐶^2 = AB . CDc) Gọi E và F lần lượt là trung điểm của AB, CD . Chứng minh: E, F, H thẳng hàngChi minh voi , minh chuyen khoan 10k momo neu ai...
Đọc tiếp
Cho ∆𝐴𝐵𝐶 𝑣𝑢ô𝑛𝑔 𝑡ạ𝑖 𝐴 ( AB < AC ) có đường cao AH. Qua C vẽ đường thẳng song song với AB cắt tia AH tại D. Cho AB = 15cm, AC = 20cm.
a) Chứng minh ∆𝐴𝐻𝐵 𝑣à ∆𝐴𝐵𝐶 đồ𝑛𝑔 𝑑ạ𝑛𝑔,𝑡í𝑛ℎ 𝐵𝐶, 𝐻𝐵 , 𝐴H
b) Chứng minh 𝐴𝐶^2 = AB . CD
c) Gọi E và F lần lượt là trung điểm của AB, CD . Chứng minh: E, F, H thẳng hàng
Chi minh voi , minh chuyen khoan 10k momo neu ai giup minh.
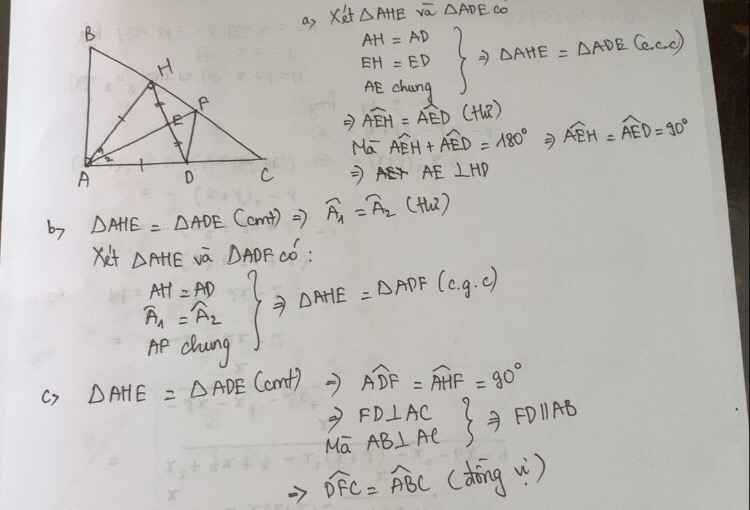
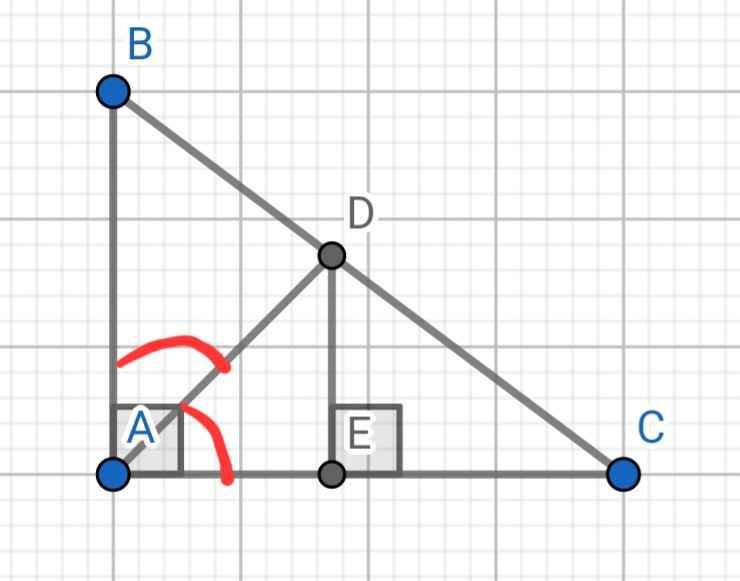
a) Xét ΔABC và ΔHBA có
ˆBAC=ˆBHA(=900)BAC^=BHA^(=900)
ˆABHABH^ chung
Do đó: ΔABC∼ΔHBA(g-g)
b) Áp dụng định lí pytago vào ΔABC vuông tại A, ta được:
BC2=AB2+AC2BC2=AB2+AC2
⇔BC2=202+152=625⇔BC2=202+152=625
hay BC=√625=25cmBC=625=25cm
Ta có: ΔABC∼ΔHBA(cmt)
⇒ACHA=BCBAACHA=BCBA
hay 15AH=252015AH=2520
⇔AH=15⋅2025=30025=12cm⇔AH=15⋅2025=30025=12cm
Vậy: BC=25cm; AH=12cm
d) Ta có: ˆCAH+ˆBAH=ˆBACCAH^+BAH^=BAC^(tia AH nằm giữa hai tia AB,AC)
⇔ˆCAD=900−ˆBAHCAD^=900−BAH^(1)
Ta có: ΔAHB vuông tại H(AH⊥BC)
nên ˆABH+ˆBAH=900ABH^+BAH^=900(hai góc nhọn phụ nhau)
hay ˆABC=900−ˆBAHABC^=900−BAH^(2)
Từ (1) và (2) suy ra ˆCAD=ˆABCCAD^=ABC^
Ta có: CD//AB(gt)
AB⊥AC(ΔABC vuông tại A)
Do đó: CD⊥AC(định lí 2 từ vuông góc tới song song)
Xét ΔBAC và ΔACD có
ˆABC=ˆCADABC^=CAD^(cmt)
ˆBAC=ˆACD(=900)BAC^=ACD^(=900)
Do đó: ΔBAC∼ΔACD(g-g)
⇒ABAC=ACCDABAC=ACCD
hay AC2=AB⋅DCAC2=AB⋅DC(đpcm)