Bài2: Tìm giái trị lớn nhất và giái trị nhỏ nhất của các hàm số sau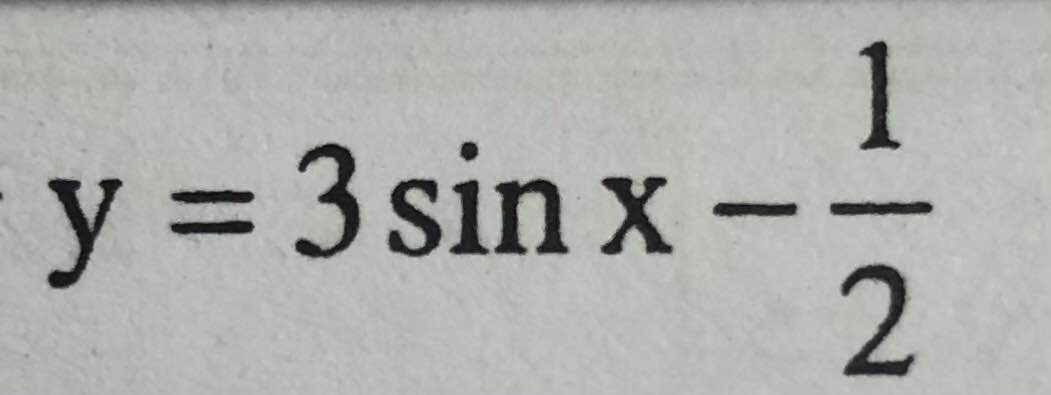
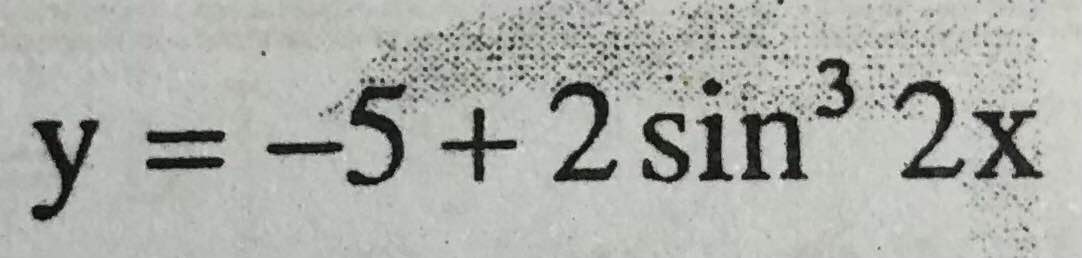
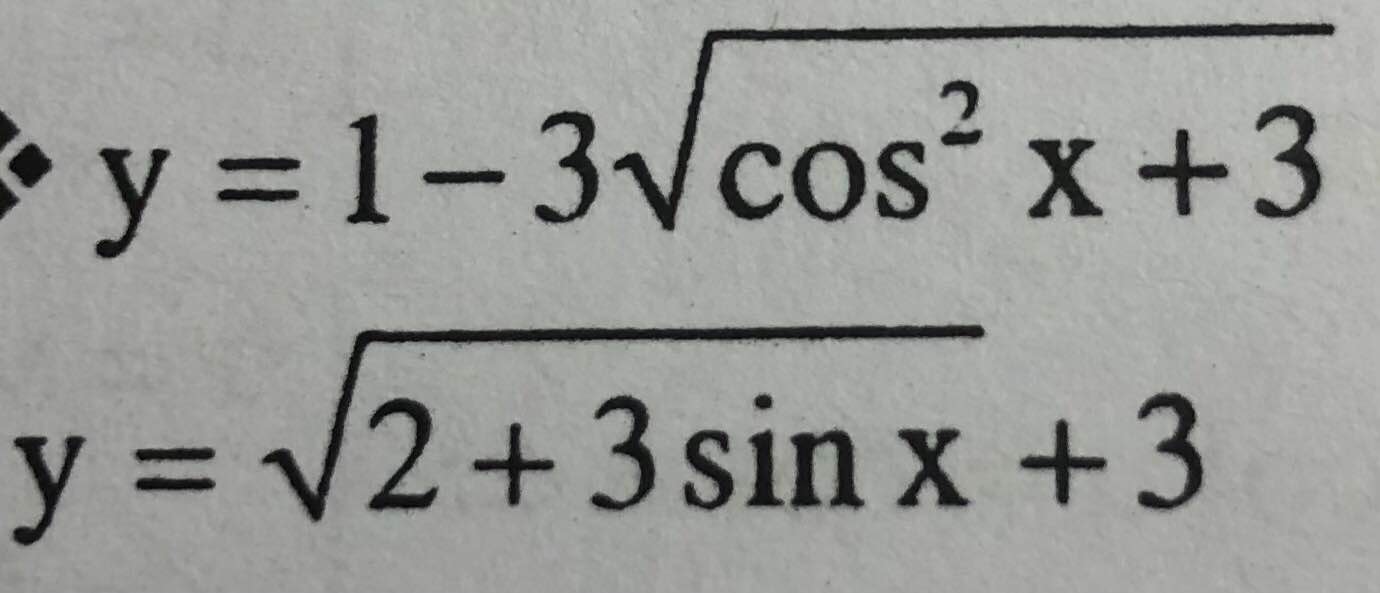
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MT
2
Những câu hỏi liên quan
CM
6 tháng 12 2017
Chọn A
Xét hàm số y = x 2 + 2 x xác định và liên tục trên 1 2 ; 2
Xét trên khoảng 
phương trình y' = 0 có nghiệm x = 1.
Vậy 
và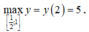 
Tích giá trị lớn nhất và giái trị nhỏ nhất của hàm số y = x 2 + 2 x trên đoạn 1 2 ; 2 bằng 15.
22 tháng 11 2023
tròi oi a viết chữ xấu wá đi à, đọc bài của a mà đau mắt wá
10 tháng 11 2016
Biến đổi \(D=\frac{4-x+10}{4-x}=1+\frac{10}{4-x}\).
D lớn nhất khi và chỉ khi \(\frac{10}{4-x}\) lớn nhất.
Xét \(x>4\) thì \(\frac{10}{4-x}< 0.\left(1\right)\)
Xét \(x< 4\) thì \(\frac{10}{4-x}>0\). Phân số \(\frac{10}{4-x}\) có tử và mẫu đều dương, tử không đổi nên có giá trị lớn nhất khi mẫu nhỏ nhất. Mẫu \(4-x\) là số nguyên dương, nhỏ nhất khi \(4-x=1\) tức là \(x=3\). Khi đó
\(\frac{10}{4-x}=10\left(2\right)\)
So sánh \(\left(1\right)\) và \(\left(2\right)\), ta thấy \(\frac{10}{4-x}\) lớn nhất bằng 10. Vậy GTLN của D bằng 11 khi và chỉ khi \(x=3\)
10 tháng 11 2016
ĐK: \(x\ne4\)
Để D lớn nhất thì 2D lớn nhất
Ta có: \(2D=\frac{2.\left(14-x\right)}{4-x}=\frac{28-2x}{4-x}=\frac{20}{4-x}+\frac{2.\left(4-x\right)}{4-x}=\frac{20}{4-x}+2\)
2D lớn nhất nên \(\frac{20}{4-x}\) lớn nhất hay 4 - x nhỏ nhất
+ Nếu x > 4 thì 4 - x < 0 => \(\frac{20}{4-x}\) < 0 (1)
+ Nếu x < 4 do 4 - x nhỏ nhất; x nguyên nên x = 3 => \(\frac{20}{4-x}=\frac{20}{4-3}=20\) (2)
So sánh (1) với (2) ta thấy (2) lớn hơn
Khi x = 3 thì \(D=\frac{14-3}{4-3}=\frac{11}{1}=11\)
Vậy GTNN của D là 11 khi x = 3
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
R
2
MH
26 tháng 1 2022
Tham khảo
y = 4sin √ x ( đk x ≥ 0 )
ta thấy: -1 ≤ sin √ x ≤ 1
<=> -4 ≤ 4sin √ x ≤ 4
<=> -4 ≤ y ≤ 4
max y = 4
dấu "=" xảy ra <=> sin √ x = 1
<=> √ x = pi/2 +2kpi
<=> x = (pi/2 +2kpi )^2
min y = -4
dấu "=" xảy ra <=> sin √ x = -1
<=> √ x = -pi/2 +2kpi
<=> x = (-pi/2 +2kpi)^2
AM
26 tháng 1 2022
a. \(y=2cos\left(x+\dfrac{\pi}{3}\right)+3\)
Ta có: \(-1\le cos\alpha\le1\)
\(\Leftrightarrow-2\le2cos\alpha\le2\)
\(\Leftrightarrow-2+3\le2cos\alpha+3\le2+3\)
\(\Leftrightarrow1\le2cos\alpha+3\le5\)
Vậy y đạt GTNN ymin=1 khi \(\left[{}\begin{matrix}x=\dfrac{2}{3}\pi+k2\pi\\x=\dfrac{-4}{3}\pi+k2\pi\end{matrix}\right.\) và y đạt GTLN khi ymax=5 khi \(x=-\dfrac{\pi}{3}+k2\pi\)
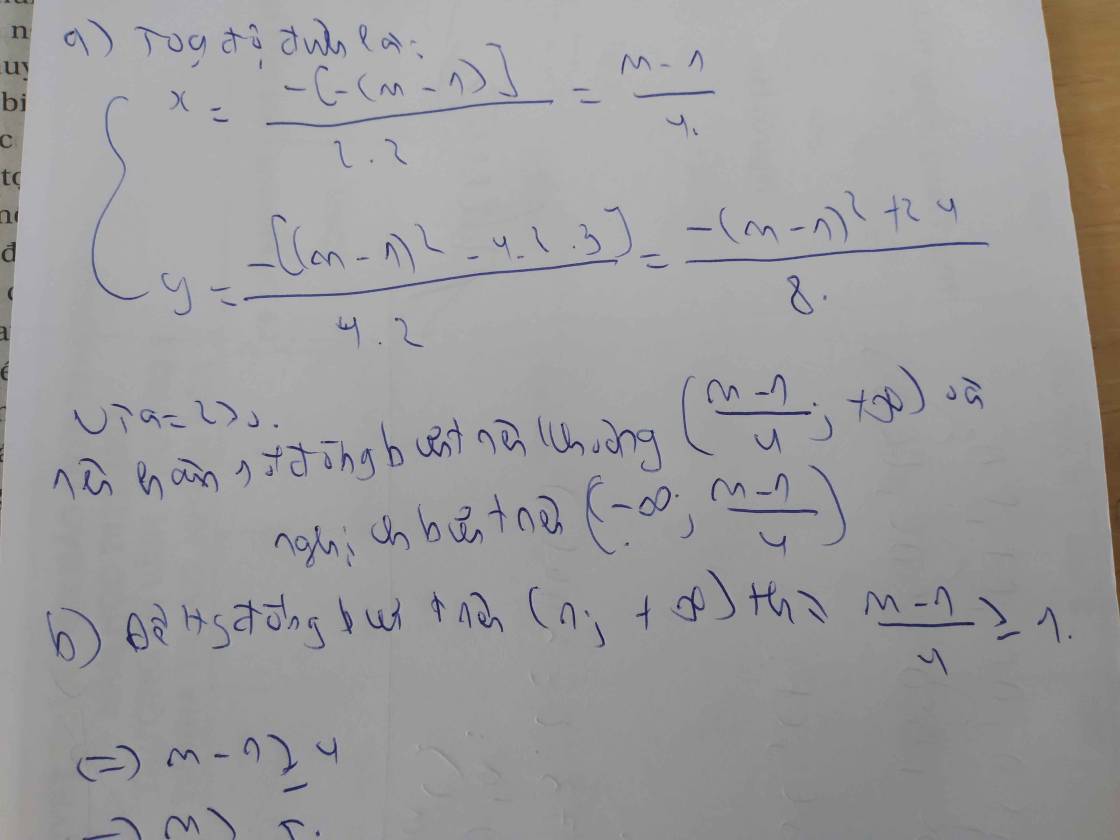
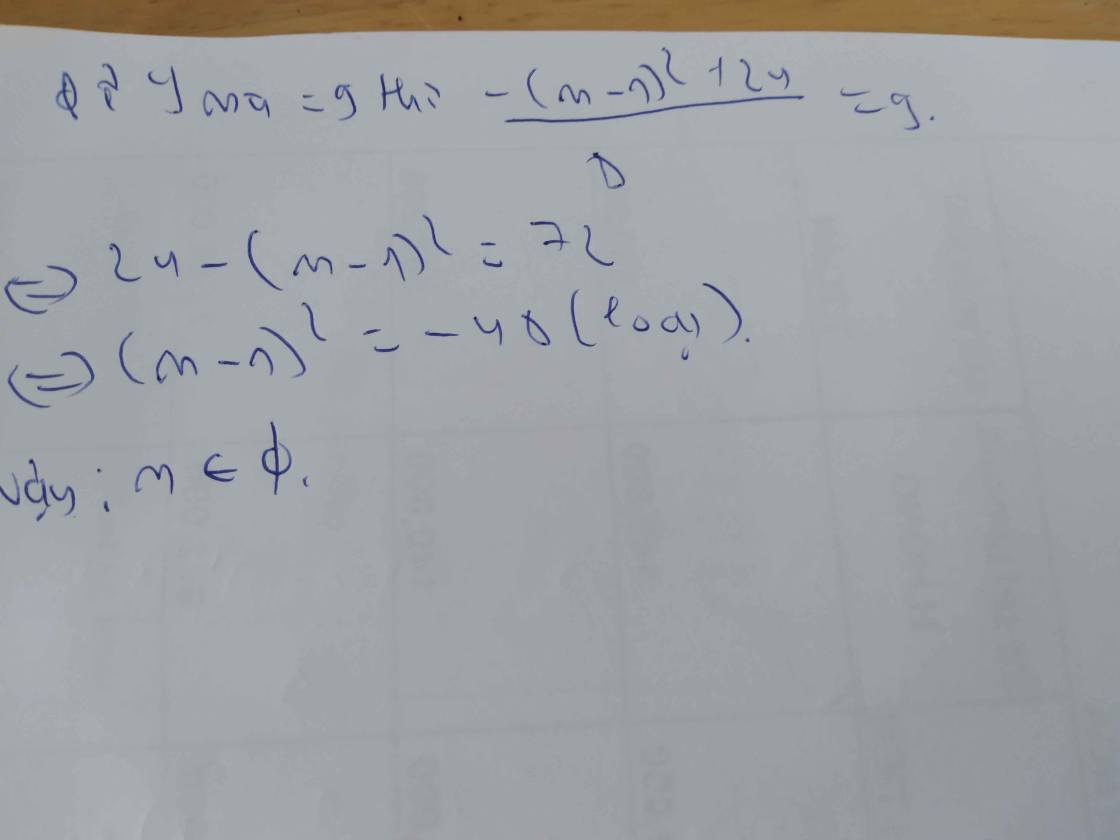
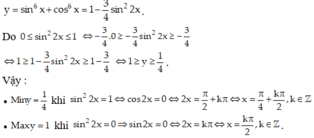
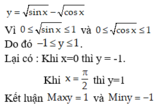
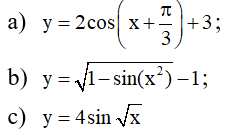
a.
\(y=3sinx-\dfrac{1}{2}\)
Do \(-1\le sinx\le1\Rightarrow-3\le3sinx\le3\)
\(\Rightarrow-\dfrac{7}{2}\le3sinx-\dfrac{1}{2}\le\dfrac{5}{2}\)
\(\Rightarrow y_{max}=\dfrac{5}{2}\) ; \(y_{min}=-\dfrac{7}{2}\)
b.
\(y=-5+2sin^32x\)
Do \(-1\le sin2x\le1\Rightarrow-1\le sin^32x\le1\)
\(\Rightarrow-2\le2sin^32x\le2\)
\(\Rightarrow-7\le y\le-3\)
\(y_{max}=-3\) ; \(y_{min}=-7\)
c.
\(0\le cos^2x\le1\Rightarrow3\le cos^2x+3\le4\)
\(\Rightarrow-2\le-\sqrt{cos^2x+3}\le-\sqrt{3}\)
\(\Rightarrow-5\le y\le1-3\sqrt{3}\)
\(y_{min}=-5\) ; \(y_{max}=1-3\sqrt{3}\)
d.
Do tính chất căn thức ta có \(\sqrt{2+3sinx}\ge0\)
\(sinx\le1\Rightarrow3sinx\le3\Rightarrow2+3sin\le5\)
\(\Rightarrow3\le y\le3+\sqrt{5}\)
\(y_{min}=3\) ; \(y_{max}=3+\sqrt{5}\)