Tìm GTLN của đa thức sau:=2x-2x2-5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2

Ta có: \(P=2x-2xy-2x^2-y^2\)
\(P=-x^2-2xy-y^2-x^2+2x\)
\(P=-\left(x^2+2xy+y^2\right)-\left(x^2-2x+1\right)+1\)
\(P=-\left(x+y\right)^2-\left(x-1\right)^2+1\)
\(P=-\left[\left(x+y\right)^2+\left(x-1\right)^2\right]+1\le1\forall x;y\)
Vậy GTLN của P là 1 khi x=-1; y=1.

Ta có: M=−x2−2x+5
=−(x2+2x−5)
=−(x2+2x+1)+6
=−(x+1)2+6
Vì −(x+1)2≤0∀x
⇒−(x+1)2+6≤6∀x
Dấu "=" xảy ra ⇔
x=−1⇔x=−1
Vậy MAXM=6⇔x=−1
Đặt A=4x−x2+3
=−x2+4x+3=−(x2−4x−3)
=−(x2−4x+4−7)
=−[(x−2)2−7]
=−(x−2)2+7
Ta có: −(x−2)2≤0⇒−(x−2)2+7≤7
Dấu " = " khi (x−2)2=0⇔x=2
Vậy MAXA=7 khi x = 2

\(A=2x-2x^2-5\)
\(A=-2\left(x^2-x\right)-5\)
\(A=-2\left(x^2-2.x.\frac{1}{2}+\frac{1}{4}\right)+\frac{1}{2}-5\)
\(A=-2\left(x-\frac{1}{2}\right)^2-4\frac{1}{2}\)
Có \(2\left(x-\frac{1}{2}\right)^2\ge0\)với mọi x
=> \(-2\left(x-\frac{1}{2}\right)^2\le0\)với mọi x
=> \(-2\left(x-\frac{1}{2}\right)^2-4\frac{1}{2}\le-4\frac{1}{2}\)với mọi x
=> \(A\le-4\frac{1}{2}\)với mọi x
Dấu "=" xảy ra <=> \(x-\frac{1}{2}=0\)<=> \(x=\frac{1}{2}\)
KL: \(A_{max}=-4\frac{1}{2}\)<=> \(x=\frac{1}{2}\)

Bài 1:
1.
$6x^3-2x^2=0$
$2x^2(3x-1)=0$
$\Rightarrow 2x^2=0$ hoặc $3x-1=0$
$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức
2.
$|3x+7|\geq 0$
$|2x^2-2|\geq 0$
Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$
$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý)
Vậy đa thức vô nghiệm.
Bài 2:
1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$
Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$
Do đó đa thức vô nghiệm
2.
$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$
$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$
Vậy đa thức khác 0 với mọi $x$
Do đó đa thức không có nghiệm.

Lời giải
Ta có
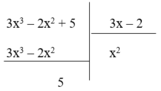
Vì phần dư R = 5 ≠ 0 nên phép chia đa thức 3 x 3 – 2 x 2 + 5 cho đa thức 3x – 2 là phép chia có dư. Do đó (I) sai
Lại có
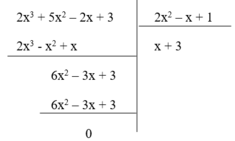
Nhận thấy phần dư R = 0 nên phép chia đa thức ( 2 x 3 + 5 x 2 – 2x + 3) cho đa thức (2 x 2 – x + 1) là phép chia hết. Do đó (II) đúng
Đáp án cần chọn là: D

a. \(A=4x-x^2+3=7-\left(x^2-4x\right)+4=7-\left(x-2\right)^2\le7\)
b.\(B=x-x^2=\frac{1}{4}-\left(x^2-x+\frac{1}{4}\right)=\frac{1}{4}-\left(x-\frac{1}{2}\right)^2\le\frac{1}{4}\)
c.\(C=2x-2x^2-5=-\frac{9}{2}-2\left(x^2-x+\frac{1}{4}\right)=-\frac{9}{2}-2\left(x-\frac{1}{2}\right)^2\le-\frac{9}{2}\)

2x - 2x2 - 5
= -2( x2 - x + 1/4 ) - 9/2
= -2( x - 1/2 )2 - 9/2 ≤ -9/2 ∀ x
Dấu "=" xảy ra <=> x = 1/2
Vậy GTLN của biểu thức = -9/2 <=> x = 1/2

\(A=-3x^2+6x-7=-3\left(x^2-2x+1-1\right)-7\)
\(=-3\left(x-1\right)^2-4\le-4\)Dấu ''='' xảy ra khi x = 1
\(B=-2x^2+5x+1=-2\left(x^2-\dfrac{5}{2}x\right)+1\)
\(=-2\left(x^2-2.\dfrac{5}{4}x+\dfrac{25}{16}-\dfrac{25}{16}\right)+1\)
\(=-2\left(x-\dfrac{5}{4}\right)^2+\dfrac{33}{8}\le\dfrac{33}{8}\)Dấu ''='' xảy ra khi x = 5/4
C;D chỉ có GTNN thôi bạn nhé \(C=2x^2-8x+13=2\left(x^2-4x+4-4\right)+13\)
\(=2\left(x-2\right)^2+5\ge5\)Dấu ''='' xảy ra khi x = 2
\(D=x^2-3x+5=x^2-2.\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}+5\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\)Dấu ''='' xảy ra khi x = 3/2
d: Ta có: \(D=x^2-3x+5\)
\(=x^2-2\cdot x\cdot\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{11}{4}\)
\(=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)