Bài 1 Cho ΔABC vuông tại A đừng trung tuyến AD và BE vuông góc với nhau tại G biết AB=\(\sqrt{6}\).Tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2018
\(\text{Xét: }\Delta BGA\perp G\text{ thì }BG^2+GA^2=AB^2\)
\(\Leftrightarrow\frac{4}{9}\left(BE^2+AD^2\right)=AB^2\)
\(\Leftrightarrow BE^2+\frac{1}{4}BC^2=\frac{27}{2}\)(1)
\(\text{Có trong: }\Delta ABE\text{ thì }AB^2+AE^2\)
\(\Leftrightarrow6+\frac{1}{4}AC^2=BE^2\)(2)
Từ (1) và (2), ta có:
\(BC^2+AC^2=30\left(cm\right)\)
Mà: \(BC^2-AC^2=AB^2=6\left(cm\right)\)
Nên \(BC^2=18\)
\(\Rightarrow BC=3\sqrt{2}\left(cm\right)\)
18 tháng 5 2018
Áp dụng Pitago cho tg ABG
Áp dụng Pitago cho tg BDG
Tiếp tục làm tiếp nha bạn :")
DD
Đoàn Đức Hà
Giáo viên
21 tháng 6 2021
Xét tam giác \(BGA\)vuông tại \(G\):
\(BA^2=BG^2+GA^2=\frac{4}{9}\left(BE^2+AM^2\right)\Leftrightarrow BE^2+\frac{BC^2}{4}=\frac{27}{2}\)(1)
Xét tam giác \(ABE\)vuông tại \(A\):
\(BE^2=AB^2+AE^2=6+\frac{1}{4}AC^2\)(2)
Từ (1) và (2) suy ra \(BC^2+AC^2=30\)
mà \(BC^2=AC^2+6\)
suy ra \(BC^2=18\Rightarrow BC=3\sqrt{2}\left(cm\right)\).
16 tháng 12 2015
Gọi G là giao điểm của AD và BE, ta có :
\(AB^2=BG.BE=\frac{2}{3}BE^2\Leftrightarrow6=\frac{2}{3}BE^2\Leftrightarrow BE=3\)
Theo định lí Pi-ta-go, ta có :
\(AE=\sqrt{BE^2-AB^2}=\sqrt{3}\Rightarrow AC=2\sqrt{3}\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{18}\)
TM
1 tháng 6 2023
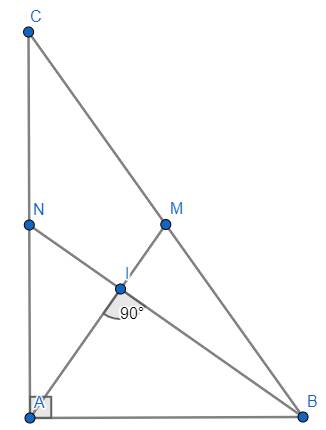
Gọi \(I\) là giao điểm của \(AM\) và \(BN\Rightarrow IB=\dfrac{2}{3}BN;IN=\dfrac{1}{3}BN;AI=\dfrac{2}{3}AM;IM=\dfrac{1}{3}AM\)
\(\Delta ANB\) vuông tại \(A:AI^2=IB.IN\) \(\Rightarrow AI^2=\dfrac{2}{3}BN\cdot\dfrac{1}{3}BN=\dfrac{2}{9}BN^2\)
Ta cũng có trong \(\Delta ANB:AB^2=IB.BN\)
\(\Leftrightarrow a^2=\dfrac{2}{3}BN\cdot BN=\dfrac{2}{3}BN^2\Leftrightarrow BN^2=\dfrac{3}{2}a^2\)
Suy ra : \(AI^2=\dfrac{2}{9}BN^2=\dfrac{2}{9}\cdot\dfrac{3}{2}a^2=\dfrac{1}{3}a^2\).
Lại có : \(AI=\dfrac{2}{3}AM\Rightarrow AM^2=\dfrac{9}{4}AI^2=\dfrac{9}{4}\cdot\dfrac{1}{3}a^2=\dfrac{3}{4}a^2\)
\(AM\) là đường trung tuyến ứng với cạnh huyền \(BC\) của \(\Delta ABC\) vuông tại \(A\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC^2=4AM^2=4\cdot\dfrac{3}{4}a^2=3a^2\)
\(\Rightarrow BC=\sqrt{3a^2}=a\sqrt{3}\)
\(\Delta ABC\) vuông tại \(A\) có : \(BC^2=AB^2+AC^2\left(Pythagoras\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{3a^2-a^2}=a\sqrt{2}\)
Vậy : \(AC=a\sqrt{2};BC=a\sqrt{3}\)
8 tháng 8 2020
gọi I là trọng tâm của tam giác ABC ta có AI vuông góc với BI
dễ thấy \(AB^2=BI\cdot BN\)
mà \(BI=\frac{2}{3}BN\)(I là trọng tâm)
\(\Rightarrow a^2=\frac{2}{3}BN^2\)
dễ thấy \(AN^2=IN\cdot BN=\frac{1}{3}BN\cdot BN=\frac{1}{3}BN^2=\frac{a^2}{2}\)
suy ra \(AC=\sqrt{2}a\)
\(BC^2=AB^2+AC^2=a^2+2a^2=3a^2\Rightarrow BC=\sqrt{3}a\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 8 2021
Đề bài thiếu, dữ liệu chỉ có thế này thì không đủ để tính BC