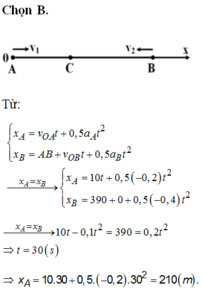Cùng lúc, trên đường thẳng có hai xe chuyển động đi qua hai vị trí A và B cách nhau 90km. Xe ô tô đi qua A chuyển động thẳng biến đổi đều với phương trình là . Xe máy đi qua B chuyển động thẳng đều với vận tốc không đổi là 72 km/h và cùng chiều với ô tô. a) Xác định vận tốc ban đầu và gia tốc chuyển động của ô tô. Từ đó nêu tính chất chuyển động của ô tô. (nhanh dần đều hay chậm dần đều, có giải thích)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 4: Hai địa điểm A, B trên một đường thẳng cách nhau 560m. Lúc 8 giờ, một xe đạp đang chuyển động thẳng đều qua A đi về phía B với vận tốc 14,4km/h. Cùng lúc đó, có một xe máy đang chuyển động thẳng nhanh dần đều từ B về A , khi qua B xe máy có tốc độ 6m/s và gia tốc có độ lớn 0,2m/s2 . a.Viết phương trình chuyển động của hai xe trong cùng một hệ qui chiếu, từ đó xác định thời điểm và vị trí hai xe gặp nhau. b.Giả sử sau khi gặp nhau, xe máy chuyển sang chuyển động thẳng đều với vận tốc bằng vận tốc khi gặp xe đạp. Hỏi khi xe đạp đến B, khoảng cách hai xe là bao nhiêu

a)Gọi \(t(h)\) là thời gian hai xe gặp nhau.
Quãng đường xe thứ nhất đi: \(S_1=50t\left(km\right)\)
Quãng đường xe thứ hai đi: \(S_2=v_2t=40t\left(km\right)\)
Hai xe chuyển động cùng chiều và gặp nhau nên:
\(50t=10+40t\Rightarrow t=1h\)
Hai xe gặp nhau lúc \(7h+1h=8h\)
b)Quãng đường xe 1 đi được đến khi gặp xe 2 là:
\(S_1=v_1t=50\cdot1=50km\)
c)Gọi \(t'\left(h\right)\) là thời gian hai xe cách nhau 20km là:
\(50t-40t=20\Rightarrow t=2h\)
Vậy hai xe cách nhau lúc \(7h+2h=9h\)

chọn \(Ox\equiv AB,O\equiv A,\) mốc tgian lúc 7h, chiều(+) A->B
\(\Rightarrow\left\{{}\begin{matrix}xA=60t\\xB=120+30t\end{matrix}\right.\)\(\left(km,h\right)\)
gặp nhau \(\Rightarrow xA=xB\Rightarrow t=4h\) gặp nhau lúc 11h
cách B \(S=30.4=120km\)

Chọn gốc tọa độ tại A.
Chọn chiều dương từ A đến B.
Gốc thời gian lúc 2 xe bắt dầu khởi hành.
a)Phương trình chuyển động của hai xe:
\(x_1=v_1t=20t\left(km\right)\)
\(x_2=20-35t\left(km\right)\)
b)Để hai xe gặp nhau: \(\Rightarrow x_1=x_2\)
\(\Rightarrow20t=20-35t\Rightarrow t=\dfrac{4}{11}h\approx0,36h\)

a)-Chọn hệ quy chiếu có chiều (+) trục Õ là từ A\(\Rightarrow\)B
-Chọn gốc toạ độ (O) tại A
-Chọn gốc thời gian (to=O)
+Xe thứ nhất có:\(\left\{{}\begin{matrix}v_{o1}=4m/s\\a_{o1}=0,2m/s^2\\x_1=0m\end{matrix}\right.\)
+Xe thứ hai có:\(\left\{{}\begin{matrix}V_{o1}=1m/s\\a_1=0,2m/s^2\\x_1=200m\end{matrix}\right.\)
-PTCĐ của xe thứ nhất và xe thứ hai lần lược là :
x=xo+vot+\(\dfrac{1}{2}\)at2
\(\Rightarrow\)x1=4t+\(\dfrac{1}{2}\).0,2t2
\(\Rightarrow\)x2=200+1.t+\(\dfrac{1}{2}\).0,1.t2
b)khi hai xe gặp nhau thì toạ đọ hai xe bằng nhau nên:
x1=x2
\(\Rightarrow\)4t+\(\dfrac{1}{2}\).0,2t2=200+1.t+\(\dfrac{1}{2}\).0,1.t2
\(\Rightarrow\)0,05t2+3t−200=0
\(\Rightarrow\)\(\left\{{}\begin{matrix}t_1=40\\t_2=-100\end{matrix}\right.\)(t1 nhận; t2 loại)
Vị trí của hai xe lúc gặp nhau là:x1=x2=200+1.40+\(\dfrac{1}{2}\).0,1.402=320(m)
vậy vị trí của hai xe lúc gặp nhau là 320m và thời gian hai xe gặp nhau là 40m/s2