Cho tam giác ABC , có G là trọng tâm . Qua G kẻ đường thẳng d sao cho d thuộc cả 2 cạnh AB, AC . Gọi H,K,N lần lượt là chân các đường vuông góc kẻ từ các góc A,B,C đến đường thẳng d . Chứng minh AH = BK + CN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2021
Gọi E là trung điểm KL; I là trung điểm AG
\(\left\{{}\begin{matrix}KE=EL\\BD=DC\end{matrix}\right.\Rightarrow ED\) là đtb hthang \(BCLK\left(BK//LC.do.cùng.\perp KL\right)\)
\(\Rightarrow ED=\dfrac{BK+CL}{2}\Rightarrow2ED=BK+CL\left(1\right)\)
Vì G là trọng tâm tam giác ABC nên \(GD=\dfrac{1}{2}AG\)
Mà \(AI=IG=\dfrac{1}{2}AG\) nên \(GD=AI=IG\)
Ta có \(ED//BK//LC\left(t/c.đtb\right)\Rightarrow ED\perp KL\left(BK\perp KL\right)\)
Áp dụng định lí Ta-lét cho \(AH//ED\left(\perp KL\right)\) ta có
\(\dfrac{AH}{ED}=\dfrac{AG}{GD}=2\Rightarrow AH=2ED\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AH=BK+CL\)
18 tháng 11 2023
1: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
=>ADHE là hình chữ nhật
=>AH=DE
2: \(\widehat{EDM}=90^0\)
=>\(\widehat{EDH}+\widehat{MDH}=90^0\)
=>\(\widehat{EAH}+\widehat{MDH}=90^0\)
=>\(\widehat{MDH}+\widehat{HAC}=90^0\)
=>\(\widehat{MDH}+\widehat{ABC}=90^0\)
mà \(\widehat{MHD}+\widehat{MBD}=90^0\)
nên \(\widehat{MDH}=\widehat{MHD}\)
=>MD=MH
\(\widehat{MDH}+\widehat{MDB}=\widehat{HDB}=90^0\)
\(\widehat{MHD}+\widehat{MBD}=90^0\)(ΔHDB vuông tại D)
mà \(\widehat{MDH}=\widehat{MHD}\)
nên \(\widehat{MDB}=\widehat{MBD}\)
=>MD=MB
=>MB=MH
=>M là trung điểm của BH
\(\widehat{NED}=90^0\)
=>\(\widehat{NEH}+\widehat{DEH}=90^0\)
=>\(\widehat{NEH}+\widehat{DAH}=90^0\)
mà \(\widehat{DAH}=\widehat{C}\left(=90^0-\widehat{ABC}\right)\)
nên \(\widehat{NEH}+\widehat{C}=90^0\)
mà \(\widehat{NHE}+\widehat{C}=90^0\)(ΔHEC vuông tại E)
nên \(\widehat{NEH}=\widehat{NHE}\)
=>NE=NH
\(\widehat{NEH}+\widehat{NEC}=\widehat{CEH}=90^0\)
\(\widehat{NHE}+\widehat{NCE}=90^0\)(ΔCEH vuông tại E)
mà \(\widehat{NHE}=\widehat{NEH}\)
nên \(\widehat{NEC}=\widehat{NCE}\)
=>NE=NC
mà NH=NE
nên NC=NH
=>N là trung điểm của HC
15 tháng 9 2019
bạn vẽ hình ra thì đọc mới hiểu nha !
a) Ta có : BB' vuông góc với d ( giả thiết ) }
MM' vuông góc với d ( giả thiết ) } => BB' // MM' // CC' ( từ vuông góc đến // )
CC' vuông góc với d ( giả thiết ) }
Xét hình thang BB'C'C ( BB' // C'C - chứng minh trên ) có :
M là trung điểm BC ( AM là trung tuyến - giả thiêt ) }
MM' // BB' ; MM' // CC' ( chứng minh trên ) } => M' là trung điểm BB'CC' ( định lí )
Xét hình thang BB'C'C có :
M là trung điểm BC ( AM là trung tuyến ) }
M' là trung điểm B'C' ( chứng minh trên ) } => MM' là đường trung bình của hình thang BB'C'C ( định lí )
=> MM' = BB' + CC' / 2 ( định lí )
ĐÓ MÌNH CHỈ BIẾT LÀM CÂU A) THÔI, XL BẠN NHA !!!
CM
9 tháng 1 2017
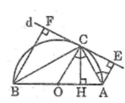
Ta có: AE // OC
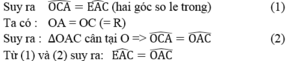
Vậy AC là tia phân giác của góc OAE hay AC là tia phân giác của góc BAE