cho tứ giác abcd.M,N lần lượt là trung điểm của AB,CD
c/m: 2MN=AC+BD=BC+AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DT
Đỗ Tươi
26 tháng 10 2016
Đúng(0)
Những câu hỏi liên quan
CM
5 tháng 12 2017
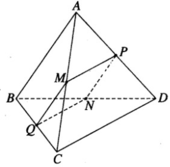
Ta có MPNQ là hình bình hành vì
Do đó
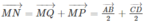
hay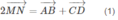 
Mặt khác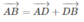 
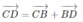
Nên
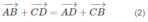
Vì
Từ (1) và (2) ta có:
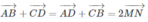
là đẳng thức cần chứng minh
MH
11 tháng 9 2021
MQ // AC (đường TB của tam giác EAC)
NP // CB (đường TB của tam giác DCB)
=> MQ // NP (vì A, C, B thẳng hàng)
=> MNPQ là hình thang
Gọi L là trung điểm DE.
Ta có LN // CE (1) (đường trung bình của tam giác DCE).
Lại có: LM // DA (2) (đường TB tam giác EAD)
Mà: AD // CE (3) (Vì góc DAC = góc ECB = 60 độ, và 2 góc này đồng vị)
Từ (1), (2) , (3) suy ra M; N; L thẳng hàng
=> MN // AD
Mà MQ // AB (c/m trên)
góc NMQ = góc DAC = 60 độ
Tương tự c/m được góc PQM = 60 độ
=> hình thang MNPQ có 2 góc kề 1 đáy bằng nhau nên là hinh thang cân
6 tháng 10 2018
Sử dụng đường trung bình, ta có: KN = 1/2 AB, NI = 1/2 CD , IM = 1/2 AB , MK = 1/2 CD
Mà AB = CD (gt)
\(\Rightarrow KN=NI=IM=MK\)
\(\Rightarrow KNIM\)là hình thoi
Do đó: MN là tia phân giác của \(\widehat{IMK}\)(tính chất hình thoi)
Chúc bạn học tốt.
27 tháng 10 2021
Xét ΔABC có
E là trung điểm của AB
N là trung điểm của AC
Do đó: EN là đường trung bình của ΔABC
Suy ra: EN//BC và \(EN=\dfrac{BC}{2}\left(1\right)\)
Xét ΔBDC có
M là trung điểm của BD
F là trung điểm của CD
Do đó: MF là đường trung bình của ΔBDC
Suy ra: MF//BC và \(MF=\dfrac{BC}{2}\left(2\right)\)
Xét ΔABD có
E là trung điểm của AB
M là trung điểm của BD
Do đó: EM là đường trung bình của ΔABD
Suy ra: \(EM=\dfrac{AD}{2}=\dfrac{BC}{2}\left(3\right)\)
Từ (1) và (2) suy ra EN//MF và EN=MF
Từ (1) và (3) suy ra EN=EM
Xét tứ giác ENFM có
EN//MF
EN=MF
Do đó: ENFM là hình bình hành
mà EN=EM
nên ENFM là hình thoi
29 tháng 7 2021
Ta có : Tứ giác MPNQ là hình bình hành
MN và PQ cắt nhau tại trung điểm I của mỗi đường
Ta có : Tứ giác EPFQ là hình bình hành
EF đi qua I
Vậy EF , MN và PQ đồng quy