1 bài thi trắc nghiệm khách quan gôm 10 câu . mỗi câu có 4 phương án trả lời . hỏi bài thi đó có bao nhiêu phương án trả lời ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2021
Tổng cộng có \(4^{10}\) khả năng xảy ra
Trong đó có đúng 1 khả năng được 10 điểm
Do đó có \(4^{10}-1\) phương án trả lời ko được 10 điểm
CM
25 tháng 12 2017
Không gian mẫu là số phương án trả lời 10 câu hỏi mà học sinh chọn ngẫu nhiên. Suy ra số phần tử của không gian mẫu là n Ω = 4 10
Mỗi câu đúng có 1 phương án trả lời, mỗi câu sai có 3 phương án trả lời. Do đó để học sinh đó trả lời đúng 7 câu: có C 10 7 . 3 3 khả năng thuận lợi.
Vậy xác suất cần tính P = C 10 7 . 3 3 4 10
Chọn C.
Cách khác. Xác suất để trả lời đúng mỗi câu là
1
4
xác suất trả lời sai mỗi câu là
3
4
. Do đó xác suất học sinh trả lời đúng 7 câu bằng 
CM
25 tháng 11 2018
Gọi Ai là biến cố:” học sinh chọn đúng ở câu i” i= 1,2,..,20
Ta có :
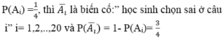
Gọi X là biến cố:” Học sinh trả lời đúng 10 câu trong 20 câu”
Số cách chọn 10 câu dúng rong 20 câu là C 20 10 = 184756
P ( X ) = C 20 10 . ( 1 / 4 ) 10 . ( 3 / 4 ) 10 = C 20 10 3 10 / 4 20
Chọn D
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 12 2022
Gọi x là số câu trả lời đúng \(\Rightarrow50-x\) câu trả lời sai
Số điểm đạt được:
\(0,2.x-0,05\left(50-x\right)=4,5\)
\(\Rightarrow x=28\)
Vậy học sinh đó trả lời đúng 28 câu và trả lời sai 22 câu
Có \(C_{50}^{28}\) cách chọn 28 câu từ 50 câu
Ở mỗi câu, học sinh có \(\dfrac{1}{4}\) xác suất trả lời đúng và \(\dfrac{3}{4}\) xác suất trả lời sai
Do đó, xác suất học sinh đó được 4,5 điểm là:
\(C_{50}^{28}.\left(\dfrac{1}{4}\right)^{28}.\left(\dfrac{3}{4}\right)^{22}=...\)
có phải 10 phương án ko